Davidson Missouri W
From 2007.igem.org
Wideloache (Talk | contribs) |
Wideloache (Talk | contribs) |
||
| Line 91: | Line 91: | ||
==[[Splitting Genes for HPP]]== | ==[[Splitting Genes for HPP]]== | ||
| - | ==[[Davidson | + | ==[[Davidson's First HPP Construct]]== |
| + | [[Image:3N graph.jpg|200px]] | ||
| + | |||
| + | The Davidson team has proposed building the graph shown above in our first attempt at solving the Hamiltonian Path Problem in vivo. (The Missouri Western team will likely build a similar graph, with an edge from node 3 to node 1 but no edge from node 2 to node 1.) In order to determine if a Hamiltonian Path exists in the directed graph above, we propose a plasmid design similar to that shown below. | ||
| + | |||
| + | [[Image:3N solved no polymerase.jpg|800px]] | ||
| + | |||
| + | This cartoon represents a solved arangement of our proposed construct. Between the two pairs of BioBrick restriction enzyme sites lies a region containing three DNA fragments, each flanked by hixC sites (represented by the black, jagged rectangles). Each node of the graph represents one of the following genes: GFP (Green Fluorescent Protein), Kanamycin Resistance and a transcription terminator. Each edge of the graph is included in the construct between two hixC sites. In the presence of Hin protein, flipping of the edges at hixC sites will produce random walks through the graph. When flipped into the correct orientation and located upstream of any transcription terminators, a given gene will be transcribed upon promotion from the promoter region. All random walks through the graph will be generated through flipping. However, by using the inducible T7 promoter, no phenotypes will be displayed intially. Only in the presence of T7 RNA polymerase will the T7 promoter allow for transcription. This T7 system has been shown to transcribe long regions of DNA. | ||
| + | |||
| + | |||
| + | [[Image:T7-polymerase plasmid.jpg|400px]] | ||
| + | <br> | ||
| + | |||
| + | All plasmids (now containing random walks through the graph) will first be retransformed into new competent cells that lack Hin protein (and, therefore, their flipping mechanism). Instead, these cells will contain the plasmid shown in the image above, which produces T7 RNA polymerase. | ||
| + | |||
| + | <br> | ||
| + | [[Image:3N solved polymerase.jpg|800px]] | ||
| + | |||
| + | T7 RNA polymerase is specific to the inducible T7 promoter on the Hamiltonian graph plasmid. Retransformation of the plasmids, therefore, has the dual effect of stopping flipping of edges and intializing transcription of all "solved" genes. The image above shows a solved plasmid post-retransformation. Both GFP and Kanamycin resistance would be expressed in this cell. | ||
| + | <br><br> | ||
| + | [[Image:3N falsepos polymerase.jpg|800px]] | ||
| + | |||
| + | It is possible for all of the genes in the graph to be expressed (or all of the nodes to be visited), but for a Hamiltonian Path not to exist in the system. A "false positive" of this type is shown above. This path (1->2, 2->1, 2->3) through the graph is not allowed because it demands "teleportation" from node 1 to node 2, and it also visits nodes (2 and 1) multiple times. Because false positives require that at least one extra edge exist in the path through the graph (when compared to true solution of the Hamiltonian Path Problem), the true solution to the HPP will always contain the shortest DNA fragment between the promoter and the terminator of all the positive phenotypes. We will screen out any false positives through PCR and gel electrophoresis. | ||
==[[Traveling Salesperson Problem?]]== | ==[[Traveling Salesperson Problem?]]== | ||
Revision as of 15:16, 29 June 2007
===Davidson & Missouri Western Team Logos, iGEM2006===
Contents |
Team Meeting Notes
Western Meeting Notes 051407 to Present [1]
Math Related Notes
Notes 051407 to Present [2]
Students
• Will DeLoache, Junior Biology Major, [3]
• Oyinade Adefuye, Senior Biology Major, [4]
• Jim Dickson, Junior Math and Economics Major, [5]
• Amber Shoecraft, Math Major, [6]
• Andrew Martens, Senior Biology Major, [7]
• Michael Waters, Sophomore Biology Major, [8]
• Jordan Baumgardner, Junior Biology, Biochemistry/Molecular Biology Major, [9]
• Tom Crowley, Senior Biochemisty/Molecular Biology Major, [10]
• Lane H. Heard, Central High School graduate, [11]
• Nickolaus Morton, Junior Chemistry Major, [12]
• Michelle Ritter, Junior Mathematics Major, [13]
• Jessica Treece, Junior Biology Major (Health Sciences), [14]
• Matthew Unzicker, Senior Biochemistry/Molecular Biology Major, [15]
• Amanda Valencia, Senior Biochem/Molecular Biology Major, [16]
Faculty
• A. Malcolm Campbell [http://www.bio.davidson.edu/people/macampbell/macampbell.html], Professor, Department of Biology, [17]
• [http://www.bio.davidson.edu/people/kahaynes/kahaynes.html Karmella Haynes], Visiting Assistant Professor, Department of Biology, [18]
• Laurie Heyer [http://www.davidson.edu/math/heyer/], Associate Professor, Department of Mathematics, [19]
Shipping Address: Malcolm Campbell, Biology Dept. Davidson College, 209 Ridge Road, Davidson, NC 28036 [(704) 894-2692]
• Todd Eckdahl [http://staff.missouriwestern.edu/~eckdahl/], Professor, Department of Biology, [20]
• Jeff Poet [http://staff.missouriwestern.edu/~poet/], Assistant Professor, Department of Computer Science, Mathematics, and Physics, [21]
Shipping Address: Todd Eckdahl, Biology Department, Missouri Western State University, 4525 Downs Drive, Saint Joseph, MO, 64507 [(816) 271-5873]
Project Overview
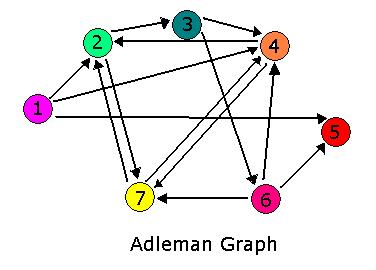
Hamiltonian Path Problem As a part of iGEM2006, a combined team from Davidson College and Missouri Western State University reconstituted a hin/hix DNA recombination mechanism which exists in nature in Salmonella as standard biobricks for use in E. coli. The purpose of the 2006 combined team was to provide a proof of concept for a bacterial computer in using this mechanism to solve a variation of The Pancake Problem from Computer Science. This task utilized both biology and mathematics students and faculty from the two institutions.
For 2007, we continue our collaboration and our efforts to manipulate E. coli into mathematics problem solvers as we refine our efforts with the hin/hix mechanism to explore another mathematics problem, the Hamiltonian Path Problem. This problem was the subject of a groundbreaking paper by Adelman in 1994 (citation below) where a unique Hamiltonian path was found in vitro for a particular directed graph on seven nodes. We propose to make progress toward solving the particular problem in vivo.
Splitting Genes for HPP
Davidson's First HPP Construct
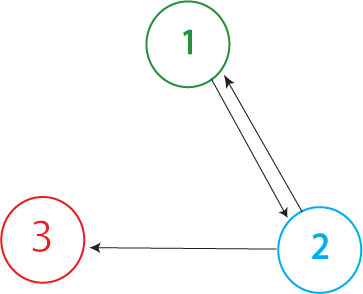
The Davidson team has proposed building the graph shown above in our first attempt at solving the Hamiltonian Path Problem in vivo. (The Missouri Western team will likely build a similar graph, with an edge from node 3 to node 1 but no edge from node 2 to node 1.) In order to determine if a Hamiltonian Path exists in the directed graph above, we propose a plasmid design similar to that shown below.
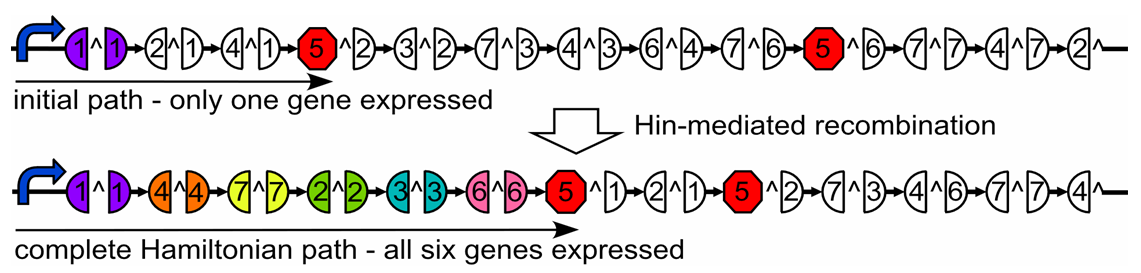
This cartoon represents a solved arangement of our proposed construct. Between the two pairs of BioBrick restriction enzyme sites lies a region containing three DNA fragments, each flanked by hixC sites (represented by the black, jagged rectangles). Each node of the graph represents one of the following genes: GFP (Green Fluorescent Protein), Kanamycin Resistance and a transcription terminator. Each edge of the graph is included in the construct between two hixC sites. In the presence of Hin protein, flipping of the edges at hixC sites will produce random walks through the graph. When flipped into the correct orientation and located upstream of any transcription terminators, a given gene will be transcribed upon promotion from the promoter region. All random walks through the graph will be generated through flipping. However, by using the inducible T7 promoter, no phenotypes will be displayed intially. Only in the presence of T7 RNA polymerase will the T7 promoter allow for transcription. This T7 system has been shown to transcribe long regions of DNA.
All plasmids (now containing random walks through the graph) will first be retransformed into new competent cells that lack Hin protein (and, therefore, their flipping mechanism). Instead, these cells will contain the plasmid shown in the image above, which produces T7 RNA polymerase.
T7 RNA polymerase is specific to the inducible T7 promoter on the Hamiltonian graph plasmid. Retransformation of the plasmids, therefore, has the dual effect of stopping flipping of edges and intializing transcription of all "solved" genes. The image above shows a solved plasmid post-retransformation. Both GFP and Kanamycin resistance would be expressed in this cell.

It is possible for all of the genes in the graph to be expressed (or all of the nodes to be visited), but for a Hamiltonian Path not to exist in the system. A "false positive" of this type is shown above. This path (1->2, 2->1, 2->3) through the graph is not allowed because it demands "teleportation" from node 1 to node 2, and it also visits nodes (2 and 1) multiple times. Because false positives require that at least one extra edge exist in the path through the graph (when compared to true solution of the Hamiltonian Path Problem), the true solution to the HPP will always contain the shortest DNA fragment between the promoter and the terminator of all the positive phenotypes. We will screen out any false positives through PCR and gel electrophoresis.
Traveling Salesperson Problem?
Resources / Citations
Missouri Western's Wet Lab Protocols
[http://gcat.davidson.edu/iGEM07/genesplitter.html Spliting Genes Web Tool]
[http://www.bio.davidson.edu/courses/Molbio/Protocols/ORIs.html Compatibility of Plasmids]
- DMW Part Numbers for 2007 are BBa_I715000 to BBa_I715999.
- [http://partsregistry.org/Help:BioBrick_Part_Names How to Name a New Part]
- [http://partsregistry.org/Add_a_Part_to_the_Registry Entering the Part to the Registry]
- [http://partsregistry.org/Help:Part_Features How to Annotate a Part]
Cool site for Breakfast [http://www.cut-the-knot.org/SimpleGames/Flipper.shtml]
Karen Acker's paper describing GFP and TetA(c) with Hix insertions [http://www.bio.davidson.edu/Courses/Immunology/Students/spring2006/Acker/Acker_finalpaperGFP.doc]
Bruce Henschen's paper describing one-time flippable Hix sites [http://www.bio.davidson.edu/Courses/genomics/2006/henschen/Bruce_Finalpaper.doc]
Intro to Hamiltonian Path Problem and DNA [http://www.ams.org/featurecolumn/archive/dna-abc2.html]
Adleman, LM. Molecular Computation of Solutions To Combinatorial Problems. Science. 11 November 1994. Vol. 266. no. 5187, pp. 1021 - 1024
Sambrook and Russell. 2001. Molecular Cloning A Laboratory Manual. Cold Spring Harbor Laboratry Press. Cold Spring Harbor, New York pg. 1.145. 2007 June.