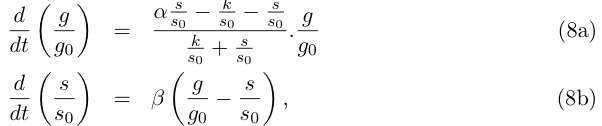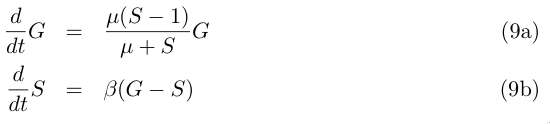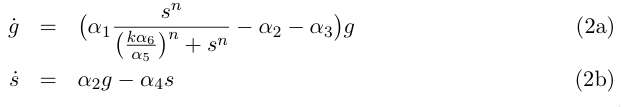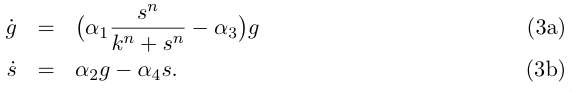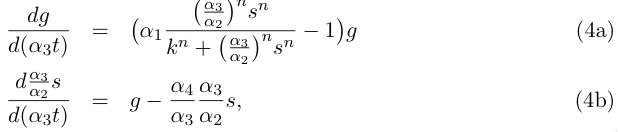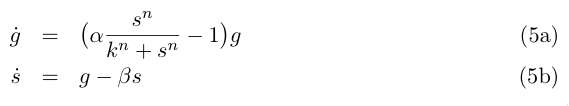Paris/Continuous model
From 2007.igem.org
Well mixed population model
We present here a theoretical approach based on population dynamics. We consider here the case of a well mixed, homogenous, culture of the SMB organism, i.e. there is no space in this analysis and we follow only the variation of the different cell lines concentrations in the culture volume.
Derivation of the model
Let the variables g, s and d describe respectively the concentrations of germinal and so-
matic cells and the conentration of DAP, then we can write for our system :
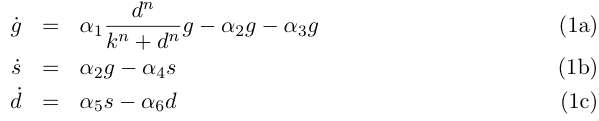
Equation (1a) describes the growth of the germinal cell population in presence of sufficient DAP (interaction represented by the Michaelis-Menten function) ; the term proportional to α2 is the differentiation into somatic cells by recombination of the CRE/LOX box, and the last term proportional to α3 is the germinal cells’ death. Equation (1b) is the variation of the somatic cells’ population, with the term proportional to α4 for somatic cells’ death. The last line describes DAP production by the somatic cells, and includes a degradation term. In absence of any quantitative details on assimilation of DAP by germinal cells and response to DAP levels, n and k are are to be considered as arbirary phenomenological parameters. We take however in the following n = 1 neglecting potential saturation related non-linearities for high DAP concentrations. The value of k corresponds to the DAP concentration for half-maximal growth rate, and could set experimenntally. We simplify the previous system by assuming that the evolution of d is rapid compared to the cellular growth, so that at this time scale we can take d' = 0 and write d = s α5/ α6 . This gives the two-variable system :
Redefinition of parameters k → kα6 /α5 and α3 → α2 + α3 leads to the simpler writing :
Let us do some rewriting :
and by redefining the time and most of the parameters we get :
The fixed points are (g = 0, s = 0) and the solution of :
Analysis of stability
2.1 Fixed point at the origin Let us linearise the equations’ system (5a) close to the origin. For small perturbations around (g = 0, s = 0) (5a) is equivalent to :