Virginia Tech/infection model
From 2007.igem.org
|
|
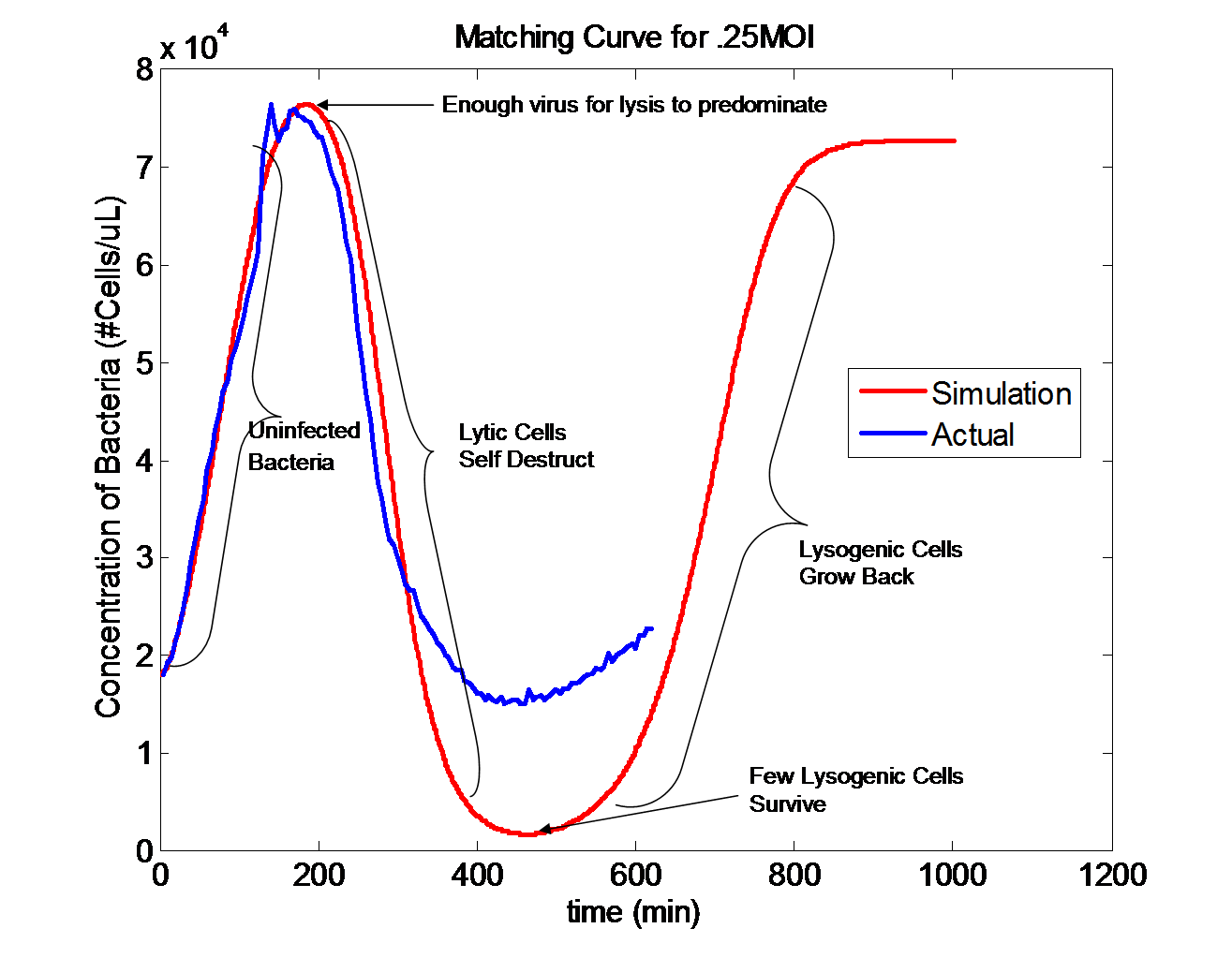
Modeling lytic and lysogenic infection phasesThe Decision Circuit for Lysogenic and Lytic Infection The probability of the cell becoming lytic or lysogenic is dependent on the ratio of phage to uninfected cells in addition to environmental factors. If there are a small number of phage viruses relative to the number of bacteria, the infected cells will have a greater probability of becoming lytic. If there are a large number of phage viruses relative to the number of bacteria, the cells will have a greater probability of becoming lysogenic. This decision circuit is decided by the multiplicity of infection (MOI) for a cell. If a single cell is infected with multiple phage viruses, this would indicate to the infected cell (and the λ genome inside it) that there is an abundance of phage in its surrounding environment and the creation of more phage would be superfluous. The cell therefore becomes lysogenic upon infection. If the cell is infected with a single phage virus, the cell has a greater probability of becoming lytic so that more phage can be introduced to the environment. Occasionally, a lysogenic cell can become lytic. If a lysogenic cell experiences stresses from the surrounding environment, it can turn lytic and release progeny phage before the cell dies.
The Simulated Infection The figure on the left shows an experimental infection curve in blue and a simulation in red. The infection occurs at .25 MOI, which means that there is one phage for every four bacteria. Since there are a significantly lower number of phage viruses in relation to uninfected bacteria, the majority of infected cells become lytic. At 200 minutes into infection, the lytic cells begin to burst releasing phage into the environment. At 400 minutes, the lytic cells have died off and a few lysogenic cells remain. Since the lysogenic cells are immune to further infection, they rapidly grow back and fill the environment.
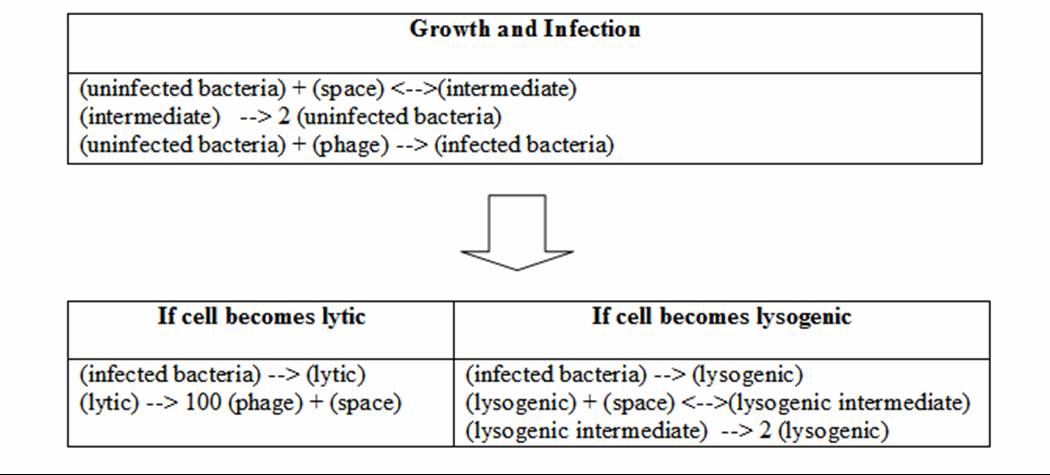
The table below shows the reaction equations that create the infection simulation curve. Space is used as a limiting substrate to inhibit the excessive growth of bacteria. When the simulation begins, there is an initial concentration of space that is steadily depleted by the bacterial growth. As lytic cells burst, the space is returned to the environment so that it is available for lysogenic growth. The lysogenic cells grow much like the uninfected cells. Monad’s derived reaction equations are used to grow the lysogenic cells as well as the uninfected cells. The reaction equations can be run with stochastic simulation; however, the simulation will not create a large variance in data. The initial concentrations for bacteria are in the thousands and at these high levels, the randomness from the stochastic simulation will not create a significant impact on the shape of the curve.
|