From 2007.igem.org

Contents 1 Spacial simulation 2 We make some hypothesis: 3 We have 3 entities in our model 4 Case 1 4.1 We produce this set of rules 4.2 Initial state 4.3 Parameters 4.4 Output

Spacial simulation

We try with this work to characterize the diffusion of the DAP and the effect on the cells. We have a growing culture with germinal cells and somatic cells.
We want to see if we can have different kinds of evolution for our cells

We make some hypothesis:

We work with a evolving population ( death for BactS and division BactG).

• Case 1 : The differentiation is DAP dependent, it's append when the cell as enough DAP to evolve but not enough to divide.
  
• Case 2 : The differentiation has a constant rate, it will be the same rate for each division cycle

The DAP is made in bacteria S, the production rate is the difference between the total production and self consummation
We consider a global variable DAP (no internal/external DAP)
The DAP is consumed in bacteria G


All the cells grow

We have 3 entities in our model

Bact it has a concentration internal of DAP and a radius. It's a cell in our automaton
BactS is a Bact which produce DAP and can grow
BactG is a Bact which consume DAP and can divide or differentiate

Case 1

We produce this set of rules

Mechanic forces

• We create a spring between the center of each Bact, then we compute the forces related to this spring and we update the position of the cells (adding noise to it)
  

For bactS

• if random < Probability of death then

BactS=null

else

if random < probability to grow & size < max cell size then

BactS=BactS+{new size=size+delta}

else

nothing

• Produce DAP

For BactG

• DAP'=DAP - self consumed DAP - diffused DAP
• if enough DAP then

if random< probability of differentiation then

BactG=BactS

else

BactG= BactG+{DAP'}

else

if size > max size then

if probability to divide > random & DAP'> minimal needed to divide then

BactG = 2 BactG with minimal size

else BactG= BactG +{DAP=DAP'}

else

if random < probability to grow then

BactG = BactG + {new size= size + delta}

else

nothing

Initial state

4 BactS and a BactG in the middle

Parameters

We have 8 parameters and we can had noise for each of them.
Mechanic

• DT time step
  
• K constant of the spring
  
• Mu variation of position
  
• R0_Gm minimal size of a BactG (after division)
• R0_G maximal size of a BactG (before division)
• R0_S maximal size of BactS

In Bact

• Diff diffusion constant
  

In BactS:

• Diffp probability of differentiation
  
• DEPOT production of DAP
  
• DeathSP probability of death
  
• CroitS probability of growth
  

In BactG:

• CONS Dap consumed
  
• DivG probability of division
  
• CroitG probability of growth
  

Output

The output is two animated pictures one showinf the differntiation the other the diffusion of DAPe

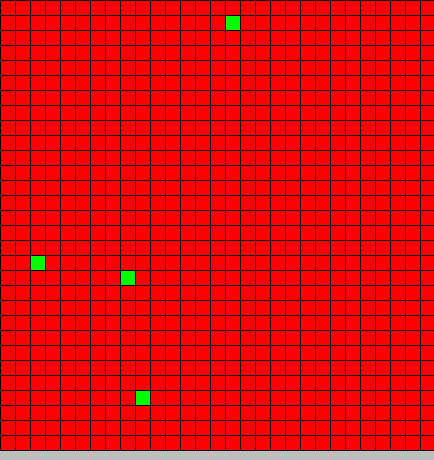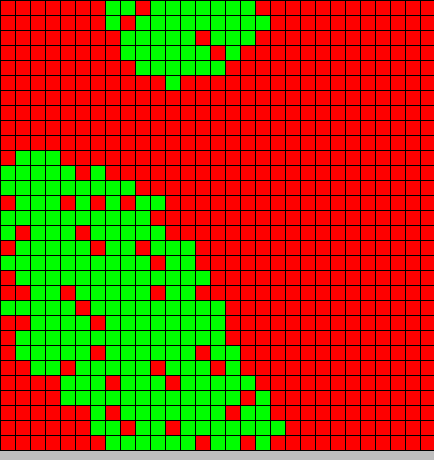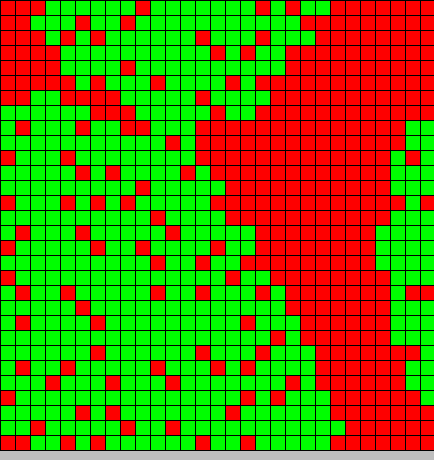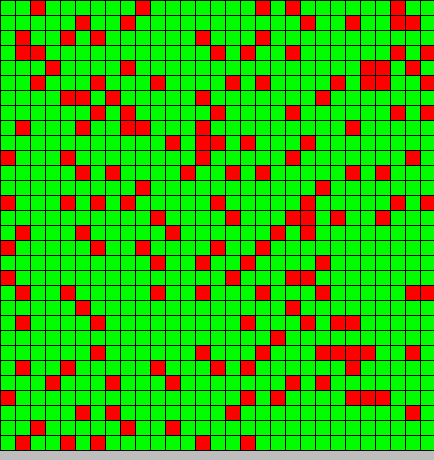
• The first picture show the diffusion of DAP

We can see a front wave in light blue after that there is a dark blue area in which the systeme is stable the concentration doesn't evolve.

• The second picture show the differention

Red BactG

Green BactS

The differentiation follow the wave front

After playing with the parameters, we can deduct 2 important things:

• The inhibition most be strong and effective (we play with the minimal and maximal value of DAP for differentiation)

if it isn't the case the system collapse all the bactG stay BactG if the inhibition is too strong or switch to BactS if the inhibition is not enough strong.

• The production and diffusion of DAP will be a critical factor

The DAP has to be produce then he will be exported, it will diffuse in the medium and will be imported

There is no proof of a special systme to import or export DAP, so for each step there is a large amount of DAP lost.