Tokyo/Formulation
From 2007.igem.org
Step1.toggle model
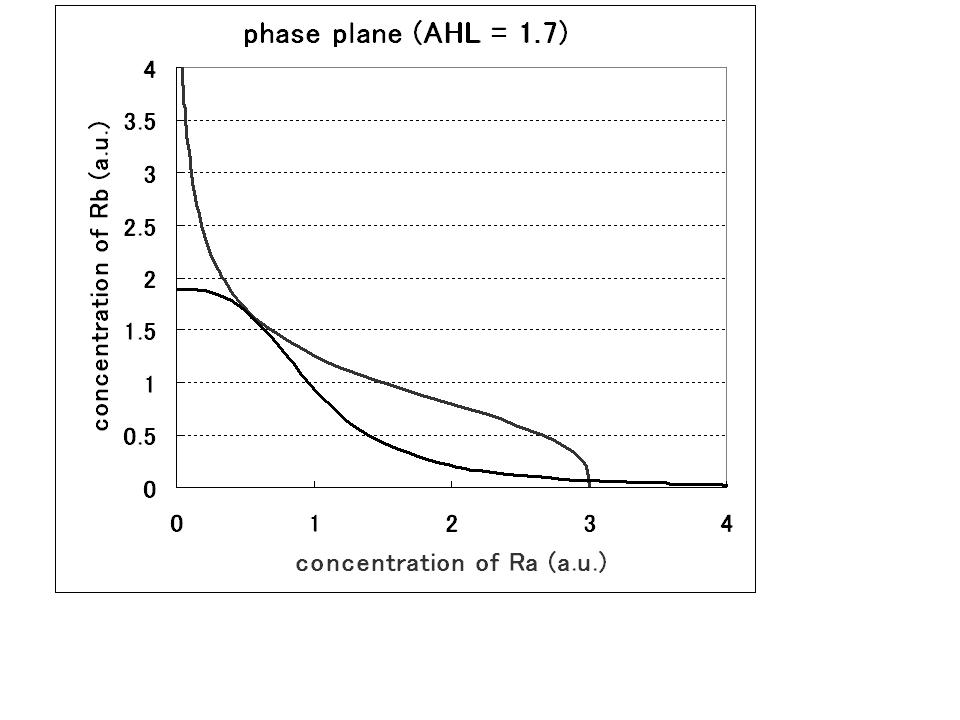
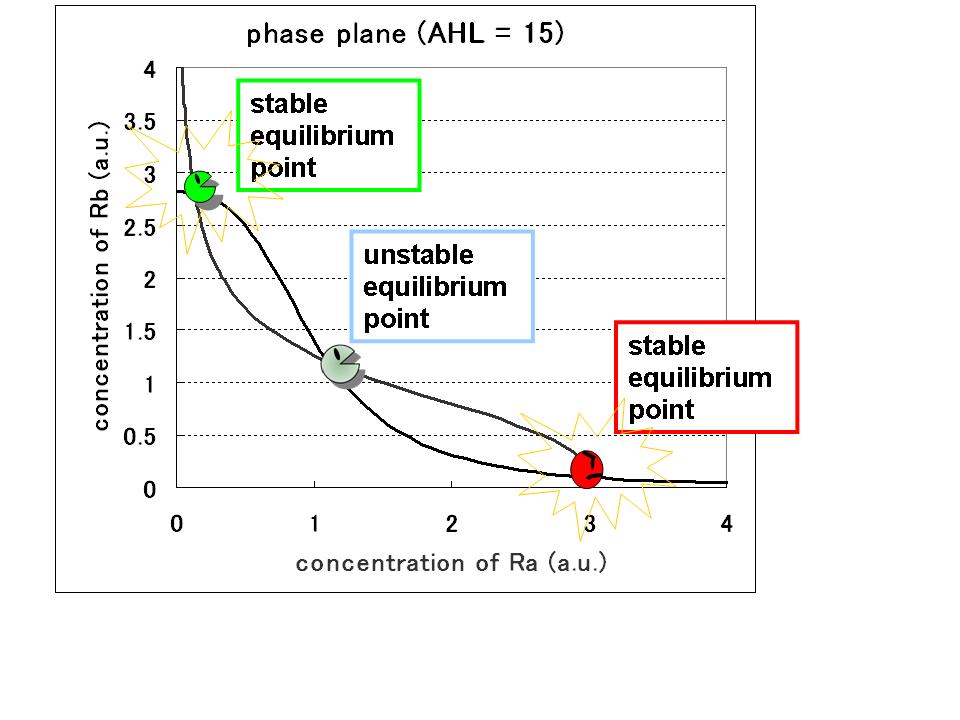
<イントロ> まずは,次元をもっていない単純な式で定性的な振る舞いをみてみる. その結果,安定点が1つのときと2つのときがある.我々が求めているモデルはA状態とB状態をとる必要があるので, 安定点が二つのときである.bistalbeになるには,パラメータにおいて,合成rateの強さ比とヒル係数が重要であることが分かった.
Step2.toggle model with hybrid promoter
<イントロ>
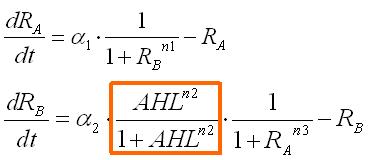
ハイブリットプロモータを式に入れ込む必要がある.
トグルの抑制項に加えてAHLによってactivateされる項が加わる.
これにより,AHL量によって相平面変化するようになる.
AHL量が少ないときはmonoで多いときトグルと同じになりbiになる.

Step3.AHL-experssing model
<イントロ>
今度は,大腸菌の中からAHLを作り出す系に拡張する.
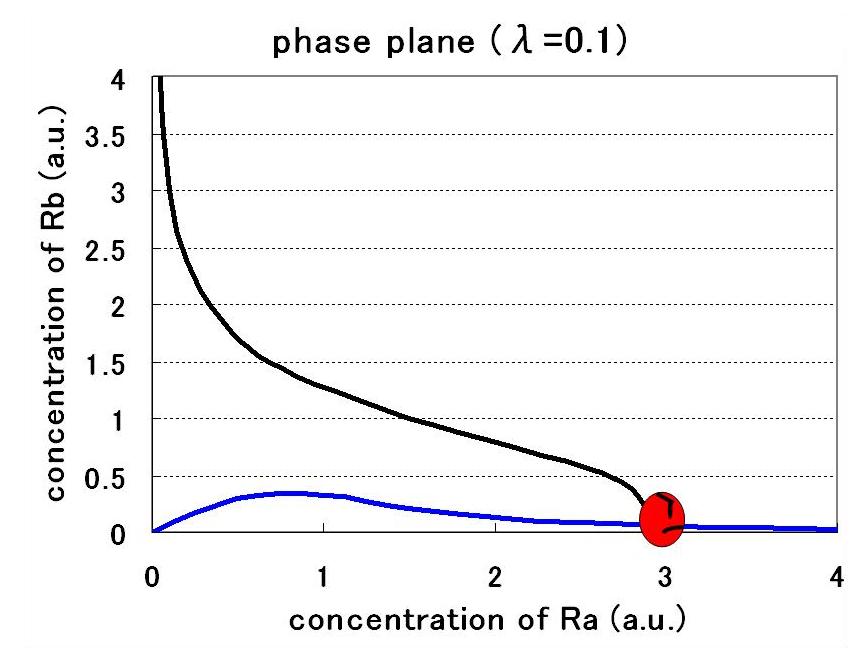
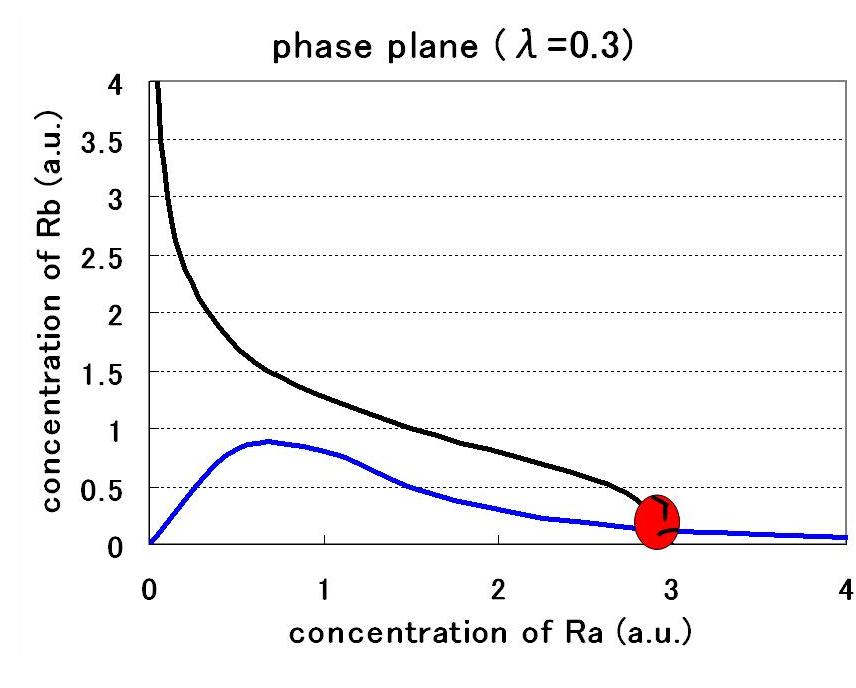
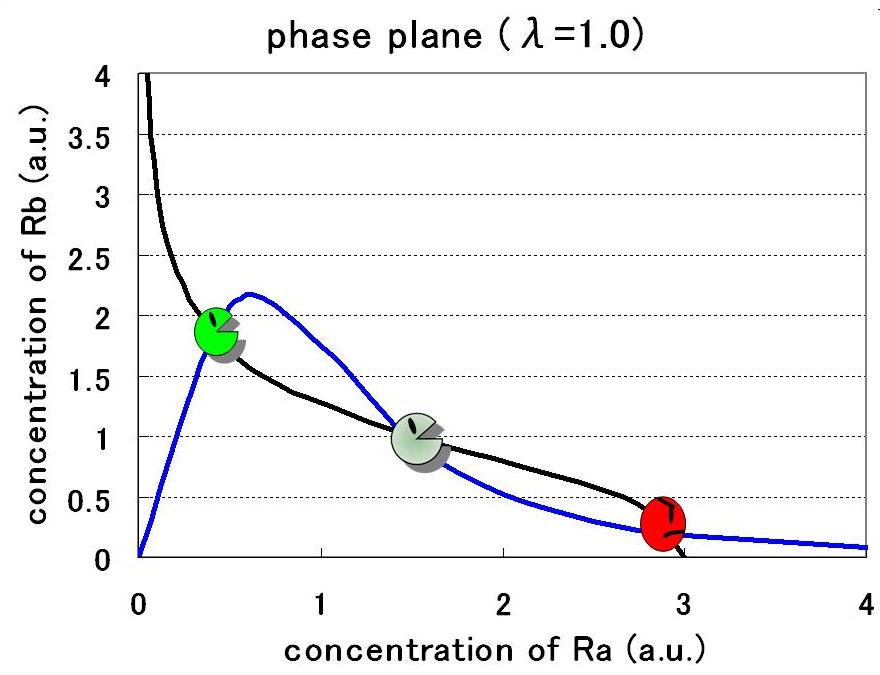
すると,nullclineが非対称になり,従来のトグルとは異なった相平面になる.
この際,新たなパラメータλが入ってくる.
パラメータセットによって,monoになったり,biになったりする.
bistableになるにはある値以上のλでなければならない.for more detail
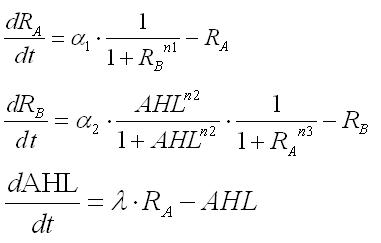
Step4.population model
<イントロ> 1個体から複数個体に拡張.AHLの式は,AHLの移動がfreelyと論文にあるので大腸菌内と外とを区別していない ここでも,相平面解析を行った.n個体の振る舞いであっても,その中の1個体に着目することで相平面解析を可能にした. この際,新たなパラメータとして個体数nがはいってくる.
ただし,deterministicなため全個体同じ動き.我々のモデルはこれではみれない. stochasticなシミュレーションが要求される.