Paris/Stochastic model
From 2007.igem.org
In this last part of the models section, we are developing a stochastic simulation of the microscopic model. The major contribution is to handle in a stochastic context a dynamic and heterogeneous population of bacteria.
Contents |
Introduction
In 1977, Gillespie developed an exact Simulation Stochastic Algorithm (SSA) dedicated to the simulation of homogeneous chemical systems. This method was recently used in many applications for the simulation of biological systems. A good point of this approach is that it allows to handle biochemical systems where numbers of molecules are low and that cannot be well characterized by classical approach using differential equations and chemical concentrations. Nevertheless this method requires strong hypotheses about the spatial homogeneity of molecules distribution. Extensions of Gillespie's SSA have been proposed to deal with compartments.
As our system is composed of a growing and heterogeneous population of bacteria, we propose to use this extension to simulate it. In the following paragraphs, we first detail the extended SSA we use and then we present some samples generated by our implementation using the set of parameters found in the numerical analysis of the model. Note that the main contribution here is in the development of the simulation algorithm.
Extended SSA
Gillespie's SSA
From a computational point of view, the Gillespie SSA relies on a discrete events simulation of chemical reactions between individual molecules. A reaction Rμ like <math>A + B \rightarrow C</math> occurs when reactants A and B meet with enough energy to produce a molecule C. The probability that this reaction occurs during an infinitesimal time is proportional to the number of molecules A and B in the system (dependence on the concentration) and a coefficient cμ called the stochastic constant (corresponding to the reaction kinetic) when reactants are uniformly distributed in the system (intuitively meaning that each couple of molecules has the same probability to meet). This probability allows to compute, given a system composing of molecules that can react with respect to reactions R1 ... RN, the probability law p(mu,tau) that the next reaction to occur is Rmu after tau units of time.
The algorithm developed by Gillespie consists in iterating the drawing of the next reaction mu to occur and the corresponding next reaction time tau using p(mu,tau) and making the system evolves. Assuming that S is chemical solution where reactions R0 ... RN can occur at a given time t, the SSA can be expressed as follows:
SSA (S,t,R0,...,RN) = {
compute mu and tau using p(mu,tau)
compute S' by applying mu on S
return (S',t+tau)
}
Handling Membranes
In the SSA, molecules have to be uniformly distributed in space. It cannot be straightly used to deal with systems that exhibit a complex spatial organization, as the system we are interested in. Taking space into account means modifying the probability law p(mu,tau) in order to take care of the localization of the reaction. Obviously, it cannot be computed in practice for any kind of organization, but it is possible to develop ad-hoc algorithms for specific organizations.
We propose to consider a population of bacteria as a nested membranes system, called compartments. The environment where bacteria live is represented by a compartment that contains molecules and bacteria, and a bacterium is then represented by a compartment that contains molecules. In each compartment, the contained elements are assumed to be uniformly distributed in space.
Extended Algorithm
The extension relies on the fact that compartments elements are uniformly organized, meaning the SSA can be used in each compartment. Intuitively, at each iteration of the new algorithm, the standard SSA is evaluated on each compartment of the system ; the compartment with the smallest reaction time is updated (with respect to the corresponding reaction) and the other compartment remain unchanged. This procedure is naturally recursive and can be expressed as follows:
ExtSSA (S,t,R0,...,RN) = {
(S',t') := SSA (S,t,R0,...,RN)
foreach compartment M of S do
let (M',tM) = ExtSSA (M,t,R0,...,RN) in
if tM < t'
then
S' := replace M by M' in S
t' := tM
done
return (S',t')
}
This algorithm is taken from [http://dx.doi.org/10.1016/j.biosystems.2006.12.009 here].
MGS Implementation
As presented [http://dx.doi.org/10.1016/j.biosystems.2006.12.009 here], the MGS language provides a specific rules application strategy implementing the SSA. We propose to implement the algorithm ExtSSA using MGS. The program (available here) is briefly described with the representation of the system, the encoding of chemical reactions and a proposition of optimization for ExtSSA.
State and Structure
First of all, our system handle different types of molecules. They are represented in MGS using symbols (back quoted strings):
-
`DAP: DAP molecules
-
`Cre: Cre molecules
-
`DAPAp: DAP sensitive promoter (inhibited form`DAPAp_i)
-
`LOXP_Box: DNA configuration of germ cells (Cre bounding form`LOXP_Box_Cre)
-
`DAP_Box: DNA configuration of somatic cells
As mentioned above, the system is represented by nested compartments. MGS provides the so-called bag, a particular data structure corresponding to multi-sets (sets where multiple occurrences of the same element are allowed) whose topology is a complete graph. In other words, each element of the bag is neighbor with all the others. From the dynamical systems point of view, the neighborhood is equivalent to a potential interaction: in bags, each element can react with all the others. This topology is then perfect to represent chemical solutions and, of course, compartments. The system is composed of 3 types of compartments defined here:
- the environment of type
Envwhere all bacteria are localized
- the germ cells of type
BactGthat must contain one molecule`LOXP_Box
- the somatic cells of type
BactSthat must contain ne molecule`DAP_Box
The value (`DAP::`DAP_Box::BactS:())::(`LOXP_Box::BactG:())::`DAP::Env:() is an example of state of the system. It is composed of two bacteria, a germ cell and a somatic cell (the somatic contain one molecule of DAP), and a molecule outside diffusing DAP molecule.
Dynamics
The chemical reactions are specified using transformation rules (see here). There are 14 different reactions embedding in two different transformations:
- transformation
inBact: this transformation specify the chemical reactions occurring in bacteria (independently if they are germ or somatic). The reactions are chemicals degradation, DAPAp promoter inhibition, differentiation and DAP production (for somatic cells only).
- transformation
inEnv: this transformation specify the chemical reactions occurring in the environment. Reactions are DAP degradation, DAP import and export (this rule actually appears ininBactto improve the efficiency of the program and to noticeably reduce the execution time).
As an example, the following rule appears in inBact:
`DAPAp, `DAP ={ C = sndOrder(K_DAPApI,1.0) }=> `DAPAp_i ;
It specifies the inhibition of the promoter DAPAp by a molecule of DAP: `DAPAp and `DAP reacts to produce `DAPAp_i, the inhibited form of `DAPAp. In the arrow, the parameter C define the stoachstic constant of this inhibition. It computed using the function sndOrder that takes as arguments
-
K_DAPApI, the kinetic constant of this reaction, and
- the volume of the cell (we assume here that the volume is always 1.0 ; volume dependence is not implemented yet).
Optimization
The previously described ExtSSA is not straightly implemented. In fact, while stochastic simulations can deal with a small number of molecules, they often exhibit limitations as they are time greedy. On the first hand, events are triggered asynchronously: only one reaction is applied at time each step. A simulation requires a lot of time steps to be significant. On the other hand, choosing the next reaction requires to draw a lot of random numbers. Unfortunately, this operation is badly time consuming and increases the execution time.
We propose to decrease the number of random numbers generations by freezing cells that do not evolve. This improvement consists in using a scheduler that stocks cells with their next reaction time in a buffer (code is available at here). At each time step, the SSA is evaluated on the environment. If the returning reaction is smaller than the smallest reaction time of the buffer, then we make the environment evolve and reaction times of cells touched by this update are recomputed and the buffer updated. On the other, if the environment evolution is slower, the fastest reaction of the buffer is applied and the corresponding cell is updated. This improved version of ExtSSA is programmed here.
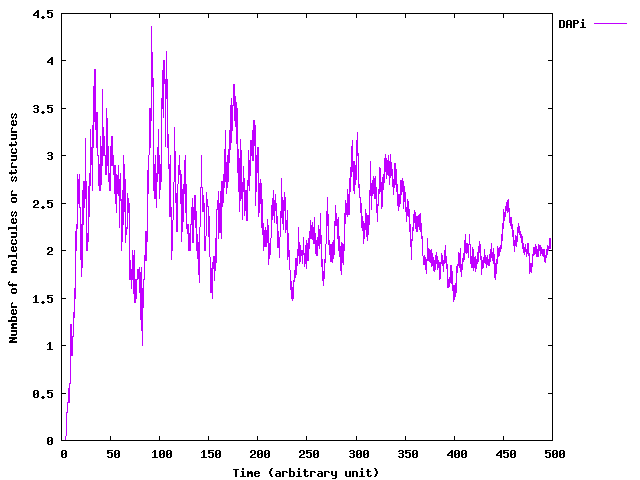
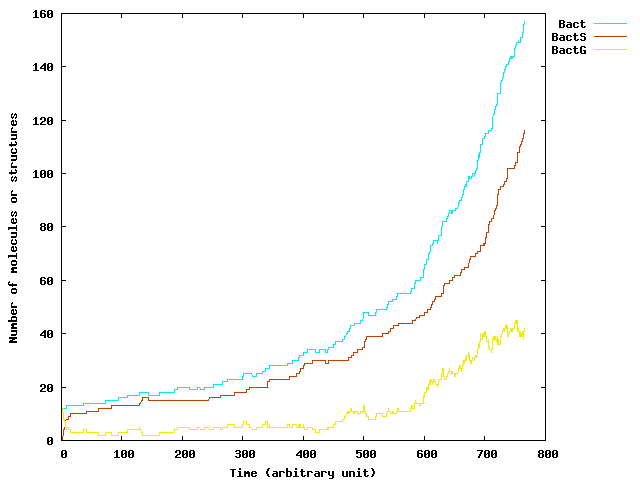
To give an idea of the efficiency of our improved algorithm, the evaluation of a 100000 steps evolution starting with a population of 20 cells to reach a population size of about 230, is about 290s on a standard computer. Moreover, note that the MGS top-level is a prototype and generic system that clearly not provides the efficiency of an ad-hoc programming of improved ExtSSA.