From 2007.igem.org

We developed simple models to evaluate the relative benefits of two different designs in term of robustness and optimization capabilities.

Contents 1 Introduction 2 Problem description 2.1 System 2.2 Expected behavior 2.3 Modeling purpose 3 Modelling 3.1 Differential equations 3.2 Parameters 3.2.1 Initial condition 3.2.2 Kinetic Parameters 3.3 Specification 4 Analysis 4.1 Robustness 4.2 Optimization

Introduction

This model aims at describing the dynamic evolution of populations of germen and soma type bacteria. It is based on a set of differential equations describing DAP synthesis, DAP transport, differentiation of germen bacteria into soma and bacteria death. This approach differs form the precedents one by the level of description of the model and the numerical analysis done on the model.

By conducting robustness and optimization analysis on two different systems, one with a constant rate of differentiation against one with a rate of differentiation driven by the concentration of DAP, we evaluate benefits and drawbacks of both systems.

We first display the consistency of the biological system by providing a set of kinetic parameters such that the numerical simulation validate a given minimal behavior. Then we analyze the system robustness with regard to its kinetic parameters and finally we try to optimize the system output by adjusting some biologically relevant parameters.

Problem description

System

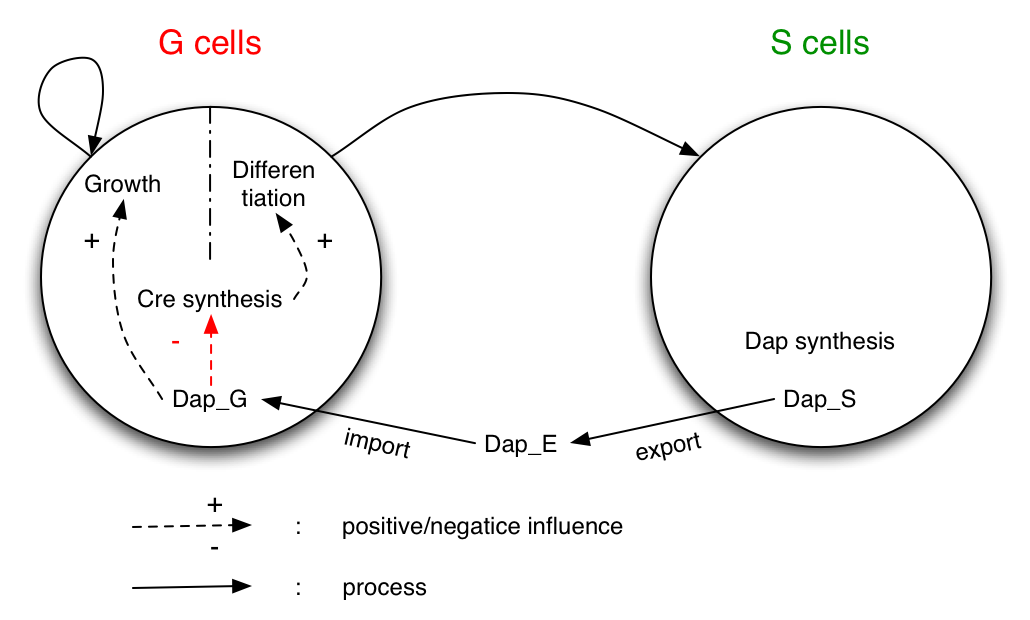
The system studied is made of two populations of bacteria G and S. Bacteria G can either divide or differentiate into S.

Dap is only synthesized by bacteria S and diffuses in the environment and in G.

G is dependent of Dap for division. Differentiation of G is controlled by Cre. Cre synthesis in G is either constant or dependant of Dap (red arrow).

Expected behavior

We consider initial conditions in which there is some bacteria G and no soma type bacteria, so that the system first has to go through an intialisation phase where a part of the initial population of G differentiate into S. Adding Dap in the environment can only have a benefic effect on the population so we choose to start this study with an initial condition lacking Dap. The requested behavior for this system is that it grows fast enough and has a robust initialization phase.

Modeling purpose

• Is minimal behavior robust ?
• How can we tune the system to improve its behavior ?
• Which system should we prefer ?

Modelling

Differential equations

To model the dependence of division and differentiation of G we use Michaelis-Menten kinetics (terms λ_div and λ_diff in equations 1 and 2). Equation (3) represents the synthesis of Cre and its degradation. We consider two models : the synthesis rate of Cre is either constant or inhibited by DAP (red term).

Term λ_div in equations (3,4) accounts for the dilution of Cre and DAP when the population of G grows.Equations involving DAP (4,5,6) represent DAP synthesis in somabacteria, DAP degradation in bacteria and in the environment, DAP transport and the release of DAP in the environment from dying bacteria. Terms λ_diff in equations (4,5) are corrective terms to take into account the mean variation of concentration of DAP in G and S when some bacteria G differentiate into S.

Parameters

We first try to find out a set of paramater values such that the system exhibits a minimal growth and a robust initialization phase. We will then use this set of parameter values as a reference point for the robustness and optimization analysis.

Initial condition

The initial condition used as reference is made of some bacteria G, no bacteria S, no Dap and no Cre.

Kinetic Parameters

In order to set parameter values we use three different methods. First, parameters λ_div and λ_death are estimations based on experimental data. Then, we fix the following inequality constraints : κ_imp > κ_exp, λ_death<λ_div, λ_diff > λ_div and γ_Dap^E < γ_Dap^GS. These inequalities express biological knowledge : Dap is actively imported into bacteria, bacteria death is lower than bacteria growth, differentiation must be lower than bacteria growth and degradation of DAP in the environment is lower than in bacteria where it is consumed. Finally we impose order of magnitude constraints to express reaction speed differences : κ_exp,κ_imp>> λ_div,λ_death,λ_diff means that transport of DAP is an order of magnitude faster than reactions modelling death, growth or differentiation of bacteria.

Based on these constraints on the parameters, we defined a set of parameter values p^* as a reference starting point.

Specification

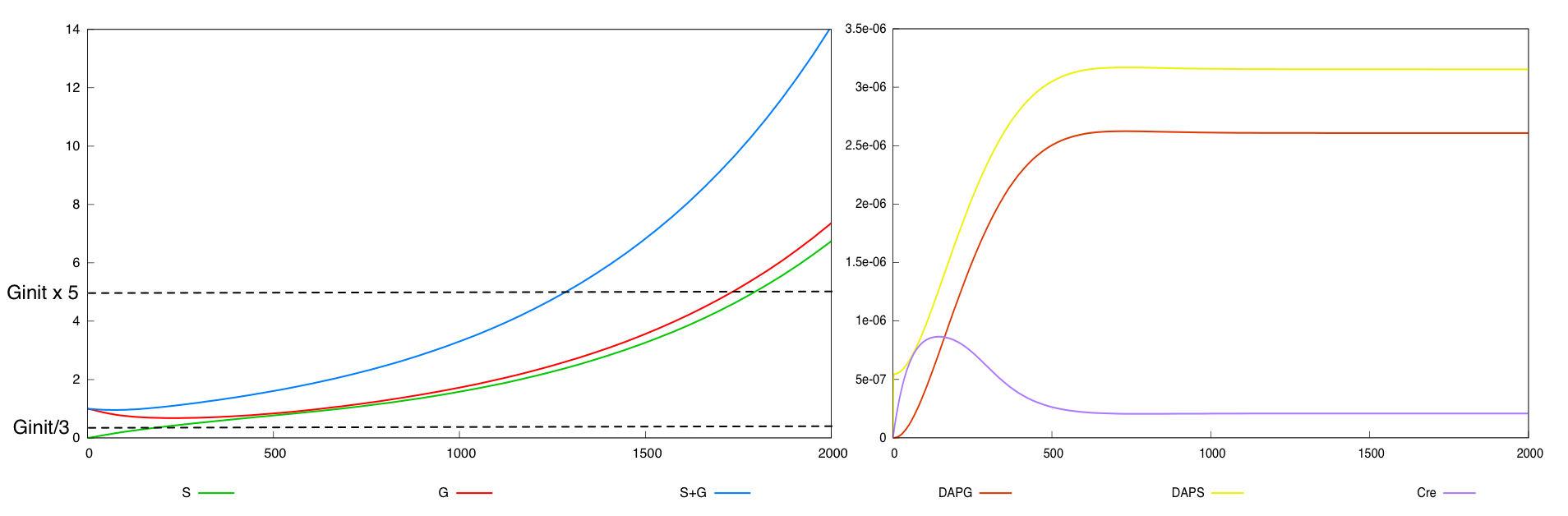
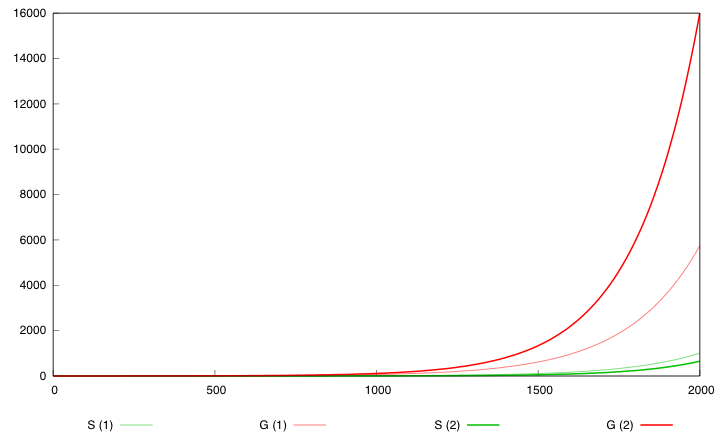
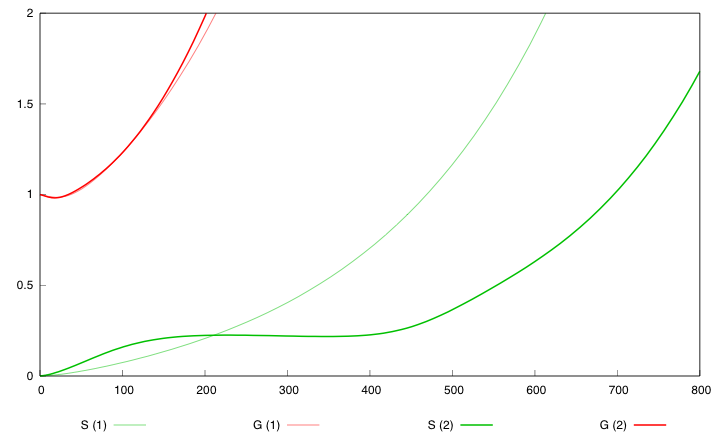
We define a minimal behavior that the system must display. First, we want that the quantity of bacteria G never falls below threshold Ginit/3. Secondly, we want that after a certain amount of time (2000 time units), the overall population of bacteria (G+S) is above threshold Ginit*5.

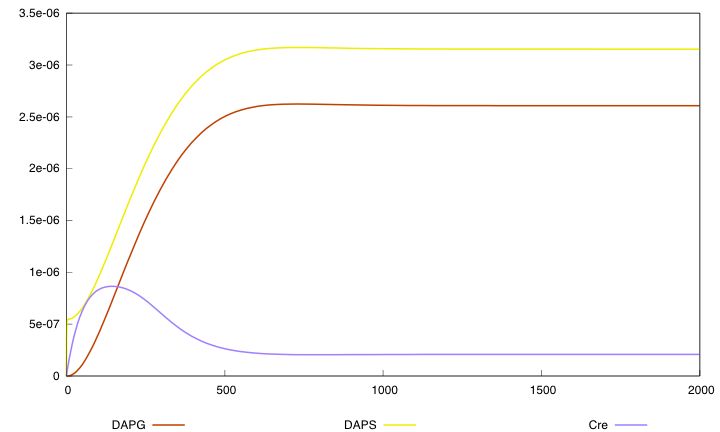
For the parmaeter values p^*, both systems validate this specification. The system with a synthesis rate of Cre dependent of Dap has the following behavior :

Analysis

Robustness

In order to evaluate the robustness of both models, we try to find a box in the parameter space containing p* such that for any point of this box the specification we defined is valid.

First of all, we reduce the number of relevant parameters to ease the enumeration process. Several parameters values act by pair, such has Kexp/Kimp determing the ratio DapE/DapGS. For each of this pairs we retained only one parameter. By using this method we extracted 9 parameters from the existing 19 parameters.

Then, to find the box we begin by searching for a box such that for any vertex of this box the system is valid, that is making 2^9 simulations and checking for everyone whether the specification is valid. Once such a box is found we sample the inner area to check if the specification is valid in the inside of the box. We sampled each parameter's interval value with 5 points.

For the system with a variable rate of synthesis of Cre the following box is valid :

	λdiff	λdiv	λdeath	κexp	θdivdap	θdiffcre	θcredap	Ginit
% decrease	20	1.5	90	50	20	8.6	30	10
% increase	10	4.6	10	100	10	100	15	1000

The system is very responsive to parameters λ_diff, λ_div and λ_death. A combined very small change of these 3 parameters int the system is enough to invalidate the required behavior.

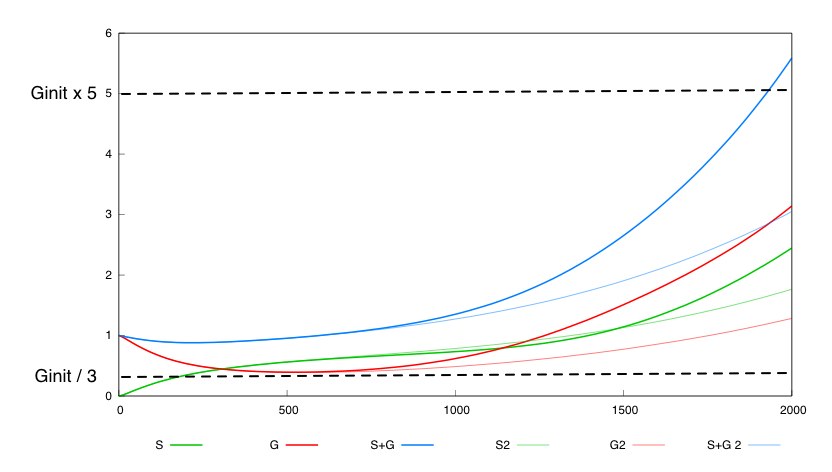
The second system with a constant synthesis rate of Cre is not valid in this whole box. 536 out of the 262000 points int this box are not valid fot this system. Here is a simulation for a given set of parameter values inside this box for which the constant rate system is not valid.

Optimization