Glasgow/DryWeek6

From 2007.igem.org

	Back To Glasgow's Main Page	Go To Glasgow's Wetlab Log

Modelling

Log

Tutorials

References

Week 6

06/08

Today we received extra data to support our estimations. General modelers meting raised issues like the further development of the model, feedback loops, or our possible influence for wet lab. Now, that we have some data, (input) we should produce some output for near future projects. Stochastics keep on runing simulations of data.

07/08

Day was full of events. First thing in the morning, we had a modelers meeting, to discuss our final model’s layout. General structure and equations were drafted on board. From now we will be analyzing previous data from lab and try to simulate new model, called Model F1.
Edinburgh team came to visit us after lunch. We exchanged some ideas about project, including modeling approaches and wet lab techniques used. After a brief introduction, we decided to continue our conversation outside the lab, so went to check what Glasgow could offer us.

08/08

Most of the day spent on Model F1, Model F1 Fedback and Model F1 Constitutive. Discussion about the stochastics full model to be able to compared with the deterministic one.

09/08

Even more types of models have been suggested to simulate. We have so much data now, so in order to manage it, we decided to document everything in LATEX. General standards are agreed for all the constants and equations. The propensities function reactions have been determinated for our stochastic model, let's go to codify them.

10/08

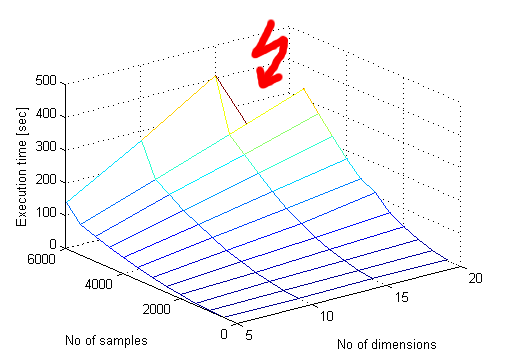
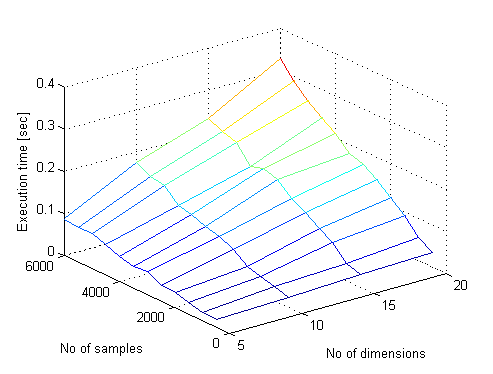
Today we realized, that even almighty MATLAB, is not always the best solution. Since our experiments require [http://en.wikipedia.org/wiki/Latin_hypercube_sampling LHS (Latin Hypercube Sampling)] in huge numbers and Matlab does it in one hour. We decided to switch back to Good Old C++. Job well done and in 10 SECONDS ONLY???!!!! What has just happened knows only Maciej himself. Only he knows The Way Of Gods.

Here I come to enlighten the oblivious. lhsdesign() in MATLAB is very slow for some reason. Moreover it seems to have polynomial complexity in number of samples while having linear complexity in number of dimensions.

Execution times for MATLAB's lhsdesign(). Slopes along x axis are straight (linear complexity), slopes along y axis are curved indicating polynomial complexity. The value for (20,6000) is unknown due to memory paging - indicated by a thunder.

At some point (e.g. 6000 samples in 20 dimensions) it also uses so much memory that a 1GB RAM Windows machine starts to page and effectively brings the computation to a halt. In the multi-parametric analysis creating a hypercube has become a limiting factor for the size of our computations. This is unacceptable!

Why do we need so many samples anyway? Well, if you take 3 dimensional space and you take 1000 samples it will be only 10 samples along each axis! What if we want to have ONLY 10 samples along each axis in 21 dimensions? Well, we'll need 1e21 samples, oh!

A quick Google search led us to a mathematical library webpage at [http://www.scs.fsu.edu/ Florida State University] where a [http://people.scs.fsu.edu/~burkardt/cpp_src/latin_random/latin_random.html C++ code for generating samples from latin hypercube] is available. A big hand for them. We have tortured the latin_random_prb.C example file to create an interface and finally call it lhsdesign.c. It takes the number of samples and number of dimensions as command line arguments and writes the samples to standard output in a format that csvread likes. Inside MATLAB the file supadupalhsdesign.m provides the same interface as lhsdesign():


function samples = supadupalhsdesign(numsamples, numdimentions)
    system(['lhsdesign.exe ', num2str(numsamples),' ', num2str(numdimentions), ' > lhsout.csv']);
    samples = csvread('lhsout.csv');
end

Execution times of the supadupalhsdesign.m averaged over 10 runs (it was a little bit shaky due to disk I/O effects). We can see that it is much faster.

What happens is the lhsdesign.exe is called using the system command and its output is directed to a temporary .csv file. Then the file is read into a matrix by csvread. Unfortunately we were not able to find a way to take the standard output of a command into a matrix directly, but it's not a major problem.

It's no rocket science, although Karolis says that rocket science is actually not so hard ;) Mcek

UPDATE 14/08: The C++ code for latin hypercube sampling wouldn't generate 200000 samples for 21 dimensions excusing itself with stack overflow. A look inside revealed that the array that stores the samples was static. A very quick


 double* x = NULL;
 x = new double[DIM_NUM*POINT_NUM];

...

 delete[] x;
 x = NULL;

fix was needed to allocate the array dynamically and our program is happy to give us 1 million samples in 23 dimensions and surely more! Mcek

Previous Week	Next Week