From 2007.igem.org

	Back To Glasgow's Main Page	Go To Glasgow's Wetlab Log

Summary

Synthetic biology has been used to describe an approach to biology which attempts to design and construct deliberate biological systems that can be investigated experimentally, which are otherwise very expensive and practically challenging. One of the central features of synthetic biology is the appreciation of the knowledge from science and engineering disciplines for the better design and understanding of synthetic networks. Here we have engineered a bacterial biosensor with the involvement of the construction of two new reporter genes PhzM and PhzS to detect polluting chemicals, which has the potential to provide an inexpensive and easy-to-use method of detecting industrial pollution. We explored a variety of computational approaches to study the behaviour of two synthetic systems: simple reporter system and positive feedback reporter system. We developed deterministic and stochastic models that quantitatively describe the graded signal-response property of the simple reporter system, and also showed that models can be expanded and used to qualitatively predict the in vivo behaviour of the complicated systems. The dynamics is further studied via the application of qualitative modelling methods. Simulations reveal that the model with positive feedback loop has higher output level than that from the intact model. This work shows that by integrating engineering techniques with scientific methodologies, we can gain a new insights into the genetic regulation and should become the reference framework for the design and construction of biochemical networks in synthetic biology.

Framework

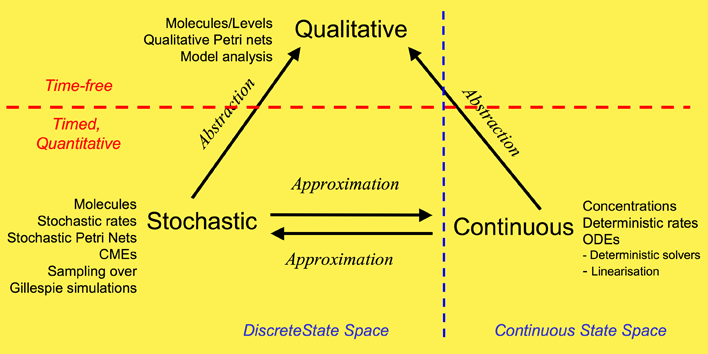
We have used a framework which unifies the qualitative, stochastic and continuous worlds, as a basis for our overall approach to modelling and analysing the biochemical pathways. Each perspective adds its contribution to the understanding of the system, thus the three approaches do not compete, but complement each other. Qualitative descriptions are abstractions over stochastic or continuous descriptions, and the stochastic and continuous models approximate each other. Note: this framework is based on (Gilbert et al 2007).

Our overall framework is illustrated in Figure 1 that relates the three major ways of modelling and analysing biochemical networks that we have used: qualitative, stochastic and continuous.

The most abstract representation of a biochemical network is qualitative and is minimally described by its topology. Initial descriptions can be obtained from biochemists, and are often in some semiformal representation. These can easily be transformed into a formal description at this stage which is usually a bipartite directed graph with nodes representing biochemical entities or reactions, or in Petri net terminology places and transitions - see Petri net section.

Figure 1. Conceptual modelling framework

The qualitative description can be further enhanced by the abstract representation of discrete quantities of species, achieved in Petri nets by the use of tokens at places. These can represent the number of molecules, or the level of concentration, of a species. A particular arrangement of tokens over a network is called a marking. The standard semantics for these qualitative Petri nets (QPN) does not associate a time with transitions or the sojourn of tokens at places, and thus these descriptions are time-free. The qualitative analysis considers however all possible behaviour of the system under any timing. The behaviour of such a net forms a discrete state space.

Timed information can be added to the qualitative description in two ways -- stochastic and continuous. The continuous model replaces the discrete values of species with continuous values, and hence is not able to describe the behaviour of species at the level of individual molecules, but only the overall behaviour via concentrations. We can regard the discrete description of concentration levels as abstracting over the continuous description of concentrations. Timed information is introduced by the association of a particular deterministic rate information with each transition, permitting the continuous model to be represented as a set of ordinary differential equations (ODEs) - see Model Evolution. The concentration of a particular species in such a model will have the same value at each point of time for repeated experiments. The state space of such models is continuous and linear. It is also possible to linearise ODE descriptions, by for example Laplace transforms, in an attempt to increase modularity in the system description and hence to facilitate model construction - see BioBrick library. This approach results in transformations from the time-domain, in which inputs and outputs are functions of time, to the frequency-domain.

The stochastic Petri net (SPN) description preserves the discrete state description, but in addition associates a particular stochastic rate information with each reaction, permitting the stochastic model to be regarded as a Markov process with a discrete state space. The time-evolution of such a process can be described by the Chemical Master Equation (CME), which is equivalent to Kolmorogov's forward equation (Wilkinson 2006). It is quite straightforward to simulate such a system, and this is usually done with the standard discrete event simulation procedure known as "the Gillespie algorithm" (Gillespie, 1977) - see Stochastic Modelling. The QPN is an abstraction of the SPN, sharing the same state space and transition relation with the stochastic model, with the probabilistic information removed. All qualitative properties valid in the QPN are also valid in the SPN, and vice versa.

In summary, the qualitative time-free description is the most basic, with discrete values representing numbers of molecules or levels of concentrations. The qualitative description abstracts over two timed, quantitative models. In the stochastic description, discrete values for the amounts of species are retained, but a stochastic rate is associated with each reaction. The continuous model describes amounts of species using continuous values and associates a deterministic rate with each reaction. These two time-dependent models can be mutually approximated by hazard functions belonging to the stochastic world.

References

D. Gilbert, M. Heiner and S. Lehrack (2007). "A Unifying Framework for Modelling and Analysing Biochemical Pathways Using Petri Nets". In proceedings Computational Methods in Systems Biology CMSB 2007 (Computational Methods in Systems Biology), Springer-Verlag LNCS/LNBI Volume 4695, pp. 200-216.

D.T. Gillespie (1977). Exact stochastic simulation of coupled chemical reactions. Journal of Physical Chemistry, 1977. 81:25 pp 2340-2361

D.J. Wilkinson (2006). Stochastic modelling for systems biology. Chapman & Hall / CRC.

Model design and analysis: outline

Figure 2. Design of our system. The intermediate compound is 5- methylphenazine-1-carboxylic acid betaine.

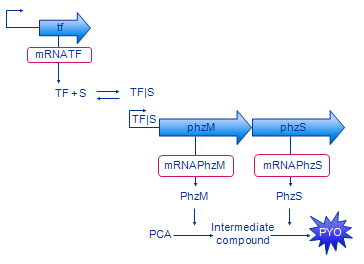
The biologists constructed an initial diagram to describe the system, using a fairly informal graphical syntax. This used a generic form of the transcription factor ('tf' for the gene, and 'TF' for the protein product) which represented both XylR (BTEX detecting) and DntR (Salicylate detecting). In outline, the steps that we used to develop and refine our model were:

1. Simplification by abstracting away the mRNA, thus combining transcription and translation.
2. Combining the PhzM and PhzS components to give one step from PCA to PYO
3. We also developed a variant of the model with a positive feedback loop

The descriptions (with and without the positive feedback loop) were then transformed into Qualitative Petri Nets (QPN) - see Petri net section. We derived the rate parameters, and wrote down descriptions and simulated the models in Ordinary Differential Equations, as well as in Continuous Petri Nets (CPN). We performed model analysis to refine the rate parameters using our implementation of the the MPSA algorithm and model comparison. Simulation of the continuous model was performed in MatLab and [http://www.bionessie.org BioNessie]. Finally we constructed and simulated stochastic models in MatLab and compared the results of from the continuous (ODE-based) and stochastic approaches.

A more detailed description of the model design process is as follows:

Model design: detailed

Figure 3. The simple model

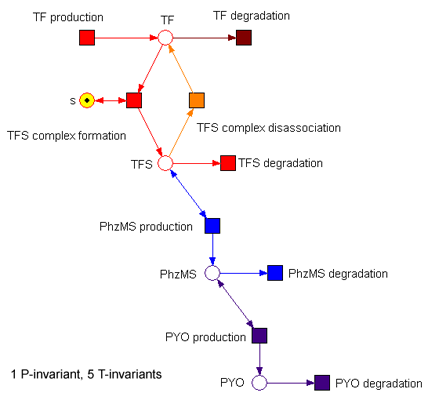
The basic design of our system is shown in Figure 2. The sensing protein TF is produced constitutively. TF stands for one of the sensing proteins that were used in the implemented system - DntR or XylR. TF, which is always present in the system, binds the signal (pollutant) compound. The TF|S complex promotes expression of the PhzM and PhzS protein coding regions. These proteins catalyse transformation of PCA compound that is available in the system into pyocyanin (PYO).

Two slightly different designs of our system were investigated in the course of the project. The latter is a modification that includes a positive feedback loop in order to enhance system's response to the signal.

Simple model

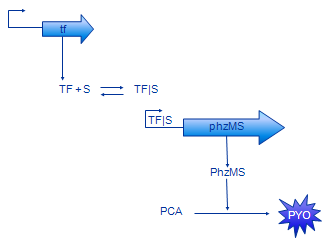
In our modelling effort we have simplified the representation of our design to ease modelling. Firstly, we have omitted the intermediate mRNA production and represented gene expression in one step instead. The resulting model contains less parameters, thus is easier to analyse. Also, there are less parameters that need to be found or estimated. In fact, gene expression rate is often measured disregarding the separation between transcription and translation.

Production of MPCAB (our working name for 5-methylphenazine-1-carboxylic acid betaine - the intermediate compound) has been dropped as well. Unfortunately, it is very hard to characterise the PCA -> MPCAB and MPCAB -> PYO reactions separately [5]. This is probably due to instability of MPCAB. The composite reaction PCA -> PYO was characterised instead. Therefore, the MPCAB has been completely removed from the model and the PhzM and PhzS proteins have been joined together into PhzMS.

The basic model is shown on the Figure 3. The equations we have developed for it are shown below.

TF protein is produced with constant rate alpha_TF and degrades at rate delta_TF. It also binds to s (pollutant) compounds with rate beta_TFS and unbinds from it with rate k_d.

The first two terms in the TFS equation are equivalent to the last two in the TF equation. The complex also degrades with rate delta_TFS.

We have used Michealis-Mented kinetics to represent production of PhzMS. This protein degrades with rate delta_PhzMS.

Pyocyanin (PYO) is produced depending on the concentration of PhzMS. It degrades with rate delta_PYO.

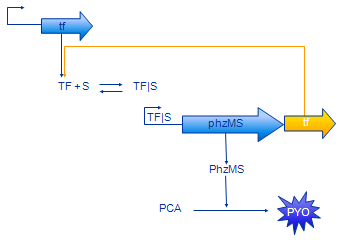
Positive Feedback Model

Figure 4. Model with positive feedback

The positive feedback model (Figure 4) includes additional coding region for TF protein placed after PhzMS coding. Once the pollutant is present and expression of reporter proteins is started also more TF is produced. Our assumption was that increased concentration of TF will cause more pollutant molecules to be bound into TF|S complex and, in turn, expression at the TF|S promoter would be enhanced further. The equations we have developed for the positive feedback loop model are as follows.

The only difference between simple model equations and feedback model equations is the term outlined in orange. It represents the additional production of TF.

It is important to note that the models share many parameters. Thanks to that comparison of the two models is much more convenient.

Simulation

Figure 5. Comparison of responses of the simple model (thin line) and feedback loop model (bold line). Pyocyanin curve is light blue, PhzMS curve is red.

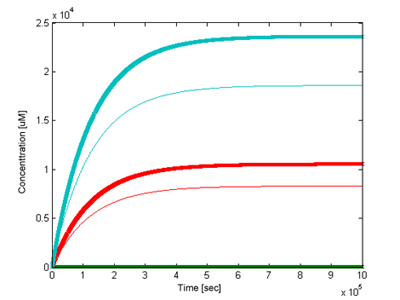
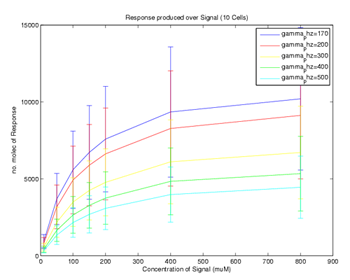
We were interested in how outputs of the two models would differ. Using the most accurate parameter values we could find (see parameter section) and signal concentration of 5uM the two models have been simulated and compared (Figure 5). Our results clearly demonstrate that the model with the positive feedback loop will give a earlier and higher response. We gave this information to the biologists who thought that this was desirable behaviour, and would take this into account in future implementations of the biological system.

Petri Net Modelling

Figure 6. The simple model in [http://www-dssz.informatik.tu-cottbus.de/index.html?/software/snoopy.html Snoopy]

[http://en.wikipedia.org/wiki/Petri_nets Petri nets] are used to describe discrete distributed systems that have concurrent processes, and provide users with an intuitive and easy-to-understand graphical representation of systems. During the iGEM project, we explored the use of Petri nets for the construction and analysis of synthetic biological networks, with a focus on facilitating the experimental design. We started off with the construction of qualitative petri-net models using the [http://www-dssz.informatik.tu-cottbus.de/index.html?/software/snoopy.html Snoopy] tool. A major advantage of the Qualitative Petri net (QPN) approach is that it enables us to perform network analysis in the absence of prior knowledge of the system parameters. We achieved this using the Charlie tool (available from [http://www-dssz.informatik.tu-cottbus.de/index.html?/software/tutorial_biopn.html Monika Heiner], where we identified the subsets of the Petri net models covered by certain properties with T-invariants (cyclic behaviour) and P-invariants (constant output in amount). We also studied various suggestions for the system's possible structures using the token game with different initial markings. Based on the observation of possible flows and discussions with biochemists, we examined and validated the models in terms of the boundedness, for example.

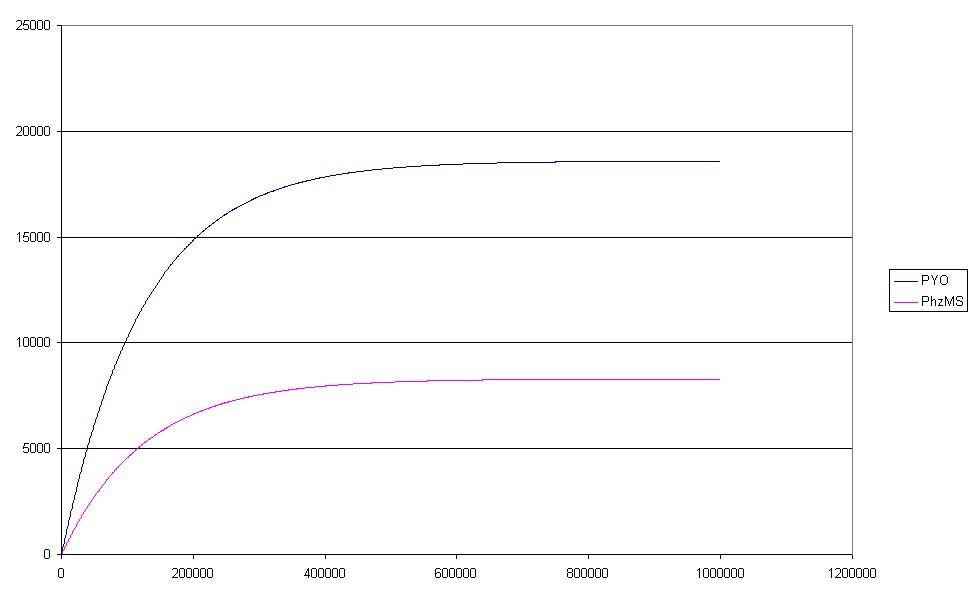
Although Petri Nets were initially designed for qualitative analysis they have been extended to permit other forms of analysis including the quantitative form which is known as a Continuous Petri Net (CPN) which has an ODE-based semantics (see framework). We investigated the dynamics of the systems quantitatively using the parameters retrieved from the literature (for details, please refer to the section on parameter searching), and simulated the behaviour using [http://www-dssz.informatik.tu-cottbus.de/index.html?/software/snoopy.html Snoopy] which can handle continuous Petri nets and has inbuilt ODE solvers. These results (see Figure below) were identical with those generated by the pure ODE approach.

For more details see the full [http://compbio.dcs.gla.ac.uk/iGEM2007/petrinets_report.pdf Petri net report].

Parameter searching and refinement

Parameter searching using Google Scholar, PubMed and biomedical databases was carried out by Christine and Xu under the direction of Dr David Leader. The task was largely steered by the discussions with, and the suggestions given by Emma Travis. We applied the Minicap program, and model comparison, both developed as part of the project, in order to help us identify sensible ranges associated with the parameters. A complete table containing either exact or constrained values for each of the system parameters was produced, as shown in the table below, where parameters are annotated with their type, values and supporting data sources.

Comparative Model Analysis

Figure 7. Plot of parameter sensitivity to difference between the simple and positive feedback model. Area between blue and red curves indicates significance of a parameter. The most significant parameter given ranges considered is gamma_PhzMS. 's' is the concentration of the input signal - polutant (constant).

In our modelling we focussed efforts on comparing the two models. In order to compare them reasonably exact parameter values are needed. In order to drive the process of refining the parameter values we have developed a method which is a simple modification of the Multi-Parametric Sensitivity Analysis.

In standard MPSA a baseline system output (from experimental data or from simulation of a model for given parameter values) is compared with model outputs for different parameter values drawn from specified parameter space.

In our modification two different models are compared for each set of parameter values from the parameter space. The values of parameters that are shared by the two models are the same for each comparison.

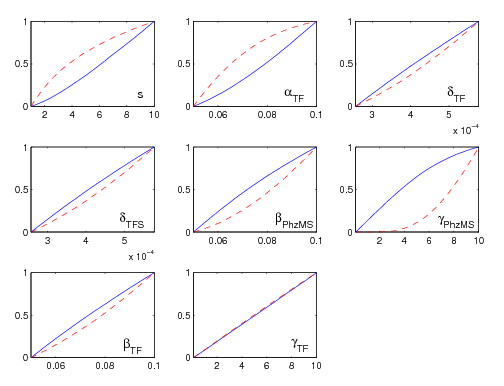
As a result the difference between the 'acceptable' and 'unacceptable' curves tells us how significant each parameter is to the difference in response of the two models.

We have modified our MPSA package and run the comparison for our two models. The parameter ranges were set according to parameter table in the Parameter searching and refinement section. The result is shown in Figure 7. Parameter gamma_PhzMS is the most sensitive one. Thus in order to refine our comparison we would first need to try to find a more accurate value for this parameter, which would involve biological experiments.

The advantage of such comparative model analysis is that it can be used identify those parameters which are worthwhile evaluating with possibly time-consuming wet-lab assays.

Minicap Sensitivity Analysis Program Package

The Multi-Parametric and Initial Concentration Sensitivity analysis package is a Matlab function which executes a chosen Dynamic or Stochastic System Function for a defined number of different variable values across any desired range. The subject of analysis can either be constants in the user's system eg. parameters in a biological system (MPSA) or initial values of the variables in the user's system eg. initial substrate concentrations (ISCSA). The program will output a plot for each variable showing a comparison of acceptable and unacceptable samples across the subject's range with 3 calculated quantitative comparison figures: the Correlation Coefficient, the Area between acceptable and unacceptable curves, and the Standard Deviation of the gradient of the acceptable plot. The comparative and intrinsic sensitivity of each chosen subject is thus highlighted. A plot showing the trend of the Substrate of Interest over time is also displayed.

As well as this report, the Minicap package contains a User Manual in html, a number of example codes and all the novel (i.e. not ode15s) function and text files required to run Minicap.

Downloads:

The MatLab source code of the Minicap is available [http://compbio.dcs.gla.ac.uk/iGEM2007/Minicap_Sensitivity_Analysis_Program_Package.zip here]. To see the full PDF report on Minicap [click here].

Stochastic Modelling

Figure 9. Stochastic simulation. 10 runs for one cell

Figure 10. Standard deviation of the parameter gamma_PhzMS

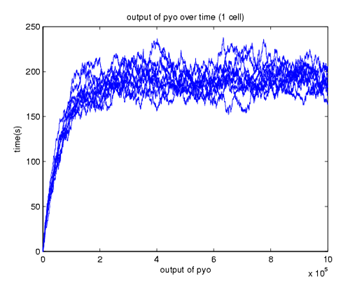
A stochastic model for a general biosensor was constructed by students and simulated using Gillespie algorithm in MATLAB. Modelling biological systems in terms of ordinary differential equations is often not enough as cells are intrinsically noisy due to low numbers of molecules that participate in reactions. This can lead to significant statistical fluctuations in reaction rates and, the systems behaviour can differ from that predicted by a deterministic model. In this case, the system of interest was a single cell or bacteria of a bacterial whole cell biosensor [1].

In this study the concept of stochastic simulation was introduced using a computational approach called Gillespie algorithm. The Gillespie algorithm allows a discrete and stochastic simulation with few reactants because every reaction is individually simulated. It takes into account a number of parameters that contribute to the model in a random manner, rather than assuming everything can be predicted. The goal of this study was to construct a stochastic model based on a deterministic one and to investigate the amount of noise (measured by the Fano factor and the coefficient of variation). Simulations were performed for several of cells and repeated for many runs to find representative behaviour. Noise was expected to decrease as the number of cells increased. However, in this study it was found that the coefficient of variation stayed roughly the same as the number of cells increased [2].

We also aimed to study whether generic features predicted by other modelling approaches can be repeated by stochastic simulations. The effects of leakiness of the promoter was also observed in the system. Leakiness had a detrimental effect on the reliability of the system. It provides a higher output of the protein which in turn gives a false indication of the level of signal being detected.

Full report on stochastic modelling
References
[1] Intrinsic noise in gene regulatory networks-Thattai and van oudenaarden
[2] Wikipedia Gillespie Algorithm-http://en.wikipedia.org/wiki/Gillespie_algorithm

Stochastic Modelling vs. ODE Modelling

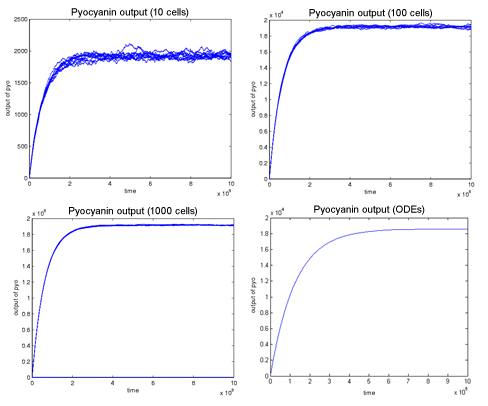
Overall, we can see that the behaviour of the stochastic model is consistent with that of the continuous (ODE) model - see Figure below. The higher the number of cells in the stochastic version the more similar the output becomes to that generated by the continuous model due to the fact that the noise decreases as the number of cells increases. However, the stochastic version output increases as the number of cells increases. This could be avoided by normalising of the graphs.

BioBrick library

BioBrickLibrary is an add-on library to Simulink for modelling dynamical biological systems at Brick (Gene) level. Simulink is a program dedicated for dynamical system simulation, however in depth knowledge of dynamics is needed if one is to simulate system mentioned above. The BioBrick library has all the blocks as well as GUI (Graphical User Interface) needed to do the job without understanding how Simulink works. It uses drag and drop system and shares all constants in Matlab’s .m file, so it is easy to store and update them.

BioBrick library’s main aim is to tell whether and how different topology will influence the output of the system. If actual rate constants are known it can be used instead or as complimentary to ODE modelling. However it must be noted that ODE rate constants ARE NOT TRANSFERABLE to BioBrick library.

Downloads:

The software is available as [http://compbio.dcs.gla.ac.uk/iGEM2007/BioBricklibrary.zip BioBrickLibrary.zip]. More information about the package can be found in ElectrEcoBluSimulinkManual document. See full Technical Report (BioBrick Type Modeling) for concept evolution and justification.

Download Models and Software

Model files

Qualitative:

Qualitative Petri net : [http://compbio.dcs.gla.ac.uk/iGEM2007/QPN_simple.spped Simple model] and [http://compbio.dcs.gla.ac.uk/iGEM2007/QPN_feedback.spped Feedback version].

Continuous:

Continuous Petri net : [http://compbio.dcs.gla.ac.uk/iGEM2007/CPN_simple.spcontped Simple model] and [http://compbio.dcs.gla.ac.uk/iGEM2007/CPN_feedback.spcontped Feedback version].

SBML : [http://compbio.dcs.gla.ac.uk/iGEM2007/iGEM_SimpleReporter.xml Simple model] and [http://compbio.dcs.gla.ac.uk/iGEM2007/iGEM_PositiveFeedbackReporter.xml Feedback version].

Matlab : [http://compbio.dcs.gla.ac.uk/iGEM2007/ODE_Basic.zip Simple model] and [http://compbio.dcs.gla.ac.uk/iGEM2007/ODE_Feedback Feedback version].

Stochastic:

Matlab: [http://compbio.dcs.gla.ac.uk/iGEM2007/stochastic_code.zip stochastic code library]

Software

Minicap program: [http://compbio.dcs.gla.ac.uk/iGEM2007/Minicap_Sensitivity_Analysis_Program_Package.zip matLab code], and report.

BioBribrick library: [http://compbio.dcs.gla.ac.uk/iGEM2007/BioBricklibrary.zip software], ElectrEcoBluSimulinkManual, and Technical Report (BioBrick Type Modeling).

BioNessie: [http://www.bionessie.org package] (a biochemical network editor, simulator and analyser for SBML descriptions, developed at the Bioinformatics Research Centre Glasgow, outwith the iGEM project).

Snoopy: [http://www-dssz.informatik.tu-cottbus.de/index.html?/software/snoopy.html package] (A Petri net tool, developed at the Brandenburg university of technology Cottbus, outwith the iGEM project).