Tokyo/Formulation
From 2007.igem.org
| (8 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| + | <br>[[Tokyo/Works|Works top]] 0.[[Tokyo/Hybrid promoter|Hybrid promoter]] 1.[[Tokyo/Formulation |Formulation]] 2.[[Tokyo/Assay |Assay]] 3.[[Tokyo/Simulation |Simulation]] 4.[[Tokyo/Assay2 |Assay2]] 5.[[Tokyo/Future works |Future works]] | ||
| + | |||
| + | |||
== [[Tokyo/Formulation/1.toggle model |Step1.toggle model]] == | == [[Tokyo/Formulation/1.toggle model |Step1.toggle model]] == | ||
<!--First,we analysis the simple dimentionless toggle model. | <!--First,we analysis the simple dimentionless toggle model. | ||
| Line 10: | Line 13: | ||
その結果,安定点が1つのときと2つのときがある.我々が求めているモデルはA状態とB状態をとる必要があるので, | その結果,安定点が1つのときと2つのときがある.我々が求めているモデルはA状態とB状態をとる必要があるので, | ||
安定点が二つのときである.bistalbeになるには,パラメータにおいて,合成rateの強さ比とヒル係数が重要であることが分かった. | 安定点が二つのときである.bistalbeになるには,パラメータにおいて,合成rateの強さ比とヒル係数が重要であることが分かった. | ||
| + | |||
| + | <!--案1 | ||
| + | <br>Introduction | ||
| + | <br>First, we saw the qualitative nature implied by simple dimentionless equations and found that the number of the stable points is one or two. Since our model must have A and B states, the number of its stable points should be two. | ||
| + | <br>For the parameters required for this bistability, we have found that the production rates and Hill coefficients are critical. | ||
| + | 上記の英語訳のPhaseplane, Threeは下の日本語訳にないです。 | ||
| + | --> | ||
| + | <!--案2 | ||
| + | <br>Introduction | ||
| + | <br>First, according to the simple dimentionless equations of our toggle, the number of equibrium points is one or two. To takes two states of A and B, our model should have two equibrium points. | ||
| + | --> | ||
== [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2.toggle model with hybrid promoter ]] == | == [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2.toggle model with hybrid promoter ]] == | ||
| Line 18: | Line 32: | ||
これにより,AHL量によって相平面変化するようになる. | これにより,AHL量によって相平面変化するようになる. | ||
AHL量が少ないときはmonoで多いときトグルと同じになりbiになる. | AHL量が少ないときはmonoで多いときトグルと同じになりbiになる. | ||
| + | <!--Factors of the hybrid promoter should be incorporated into the equations; that is, the term of the repression of toggle by LacI and that of the activation by AHL should be added. By these additions, the phase changes dependent on the amount of AHL. With few AHL, ??? --> | ||
<br>[[Image:expression2-4.jpg|300px|]][[Image:AHLresponse2-2.jpg|300px|]] | <br>[[Image:expression2-4.jpg|300px|]][[Image:AHLresponse2-2.jpg|300px|]] | ||
| Line 32: | Line 47: | ||
この際,新たなパラメータλが入ってくる. | この際,新たなパラメータλが入ってくる. | ||
パラメータセットによって,monoになったり,biになったりする. | パラメータセットによって,monoになったり,biになったりする. | ||
| + | Now develop this system to the one with cell-produced AHL. | ||
| + | This time, the nullcrine is assymetric and the phaseplane is unconventionally shaped. | ||
| + | Here the new parameter λ is introduced whether mono or bi of the system depends on the parameter sets | ||
[[Tokyo/Formulation/3.AHL-experssing model|for more detail]] | [[Tokyo/Formulation/3.AHL-experssing model|for more detail]] | ||
<br>[[Image:expression3-1.jpg|300px|]] | <br>[[Image:expression3-1.jpg|300px|]] | ||
| Line 42: | Line 60: | ||
ここでも,相平面解析を行った.n個体の振る舞いであっても,その中の1個体に着目することで相平面解析を可能にした. | ここでも,相平面解析を行った.n個体の振る舞いであっても,その中の1個体に着目することで相平面解析を可能にした. | ||
この際,新たなパラメータとして個体数nがはいってくる. | この際,新たなパラメータとして個体数nがはいってくる. | ||
| + | |||
| + | |||
| + | Here the concentration of AHL is assumed the same inside and outside of a cell according to the description that AHL is freely permiable through cell membrane in the referenced articles. In the phaseplane analysis here is mede possible by focusing on an individual in the whole. In this case, the parameter n for the number of the cells is introduced. | ||
ただし,deterministicなため全個体同じ動き.我々のモデルはこれではみれない. | ただし,deterministicなため全個体同じ動き.我々のモデルはこれではみれない. | ||
stochasticなシミュレーションが要求される. | stochasticなシミュレーションが要求される. | ||
| + | |||
| + | However, all the individuals behave in the same way in this deterministic model. To see the bahavior different from each individual, it is necessary to use stocastic simulation. | ||
== [[Tokyo/Formulation/5.poisson stochastic differential equation model |Step5.poisson stochastic differential equation model ]] == | == [[Tokyo/Formulation/5.poisson stochastic differential equation model |Step5.poisson stochastic differential equation model ]] == | ||
Latest revision as of 13:47, 23 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay 3.Simulation 4.Assay2 5.Future works
Step1.toggle model
<イントロ> まずは,次元をもっていない単純な式で定性的な振る舞いをみてみる. その結果,安定点が1つのときと2つのときがある.我々が求めているモデルはA状態とB状態をとる必要があるので, 安定点が二つのときである.bistalbeになるには,パラメータにおいて,合成rateの強さ比とヒル係数が重要であることが分かった.
Step2.toggle model with hybrid promoter
<イントロ>
ハイブリットプロモータを式に入れ込む必要がある.
トグルの抑制項に加えてAHLによってactivateされる項が加わる.
これにより,AHL量によって相平面変化するようになる.
AHL量が少ないときはmonoで多いときトグルと同じになりbiになる.
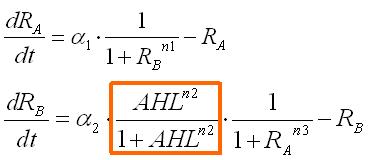

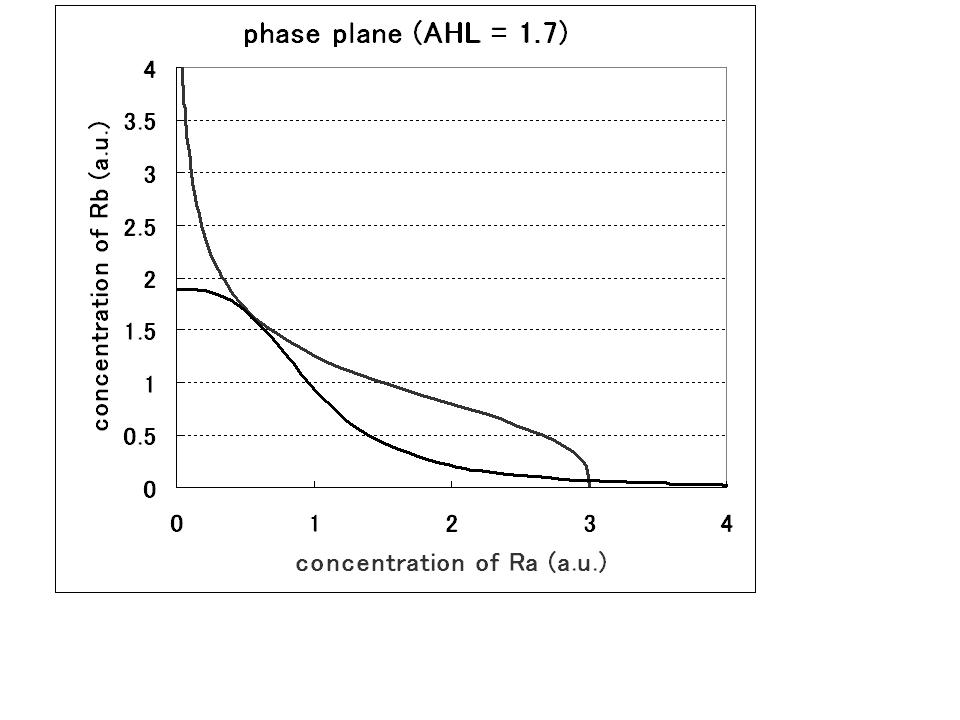
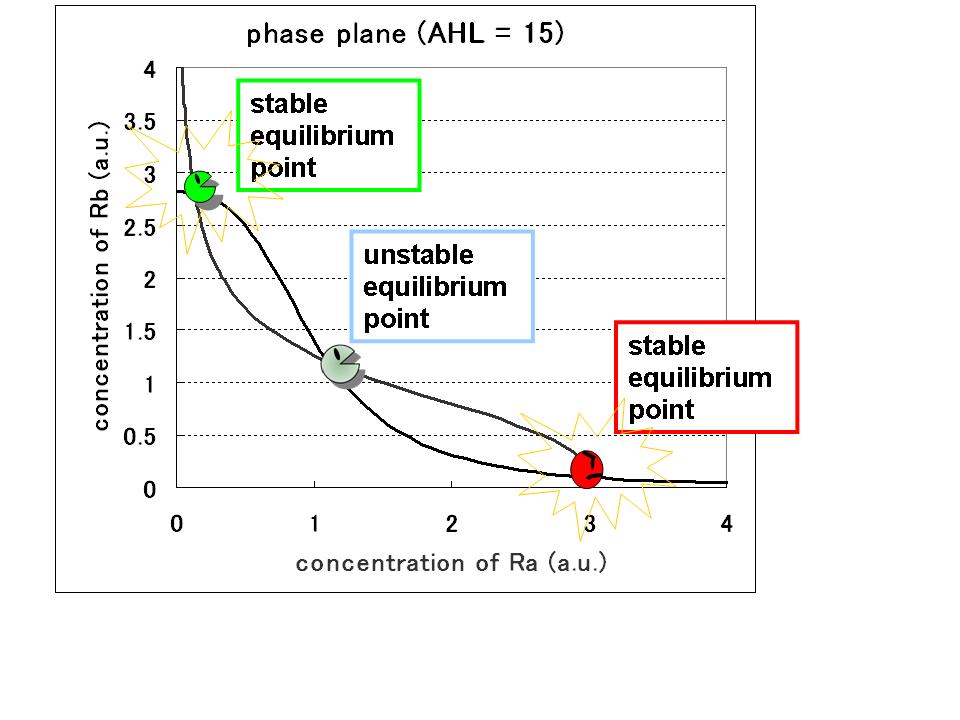
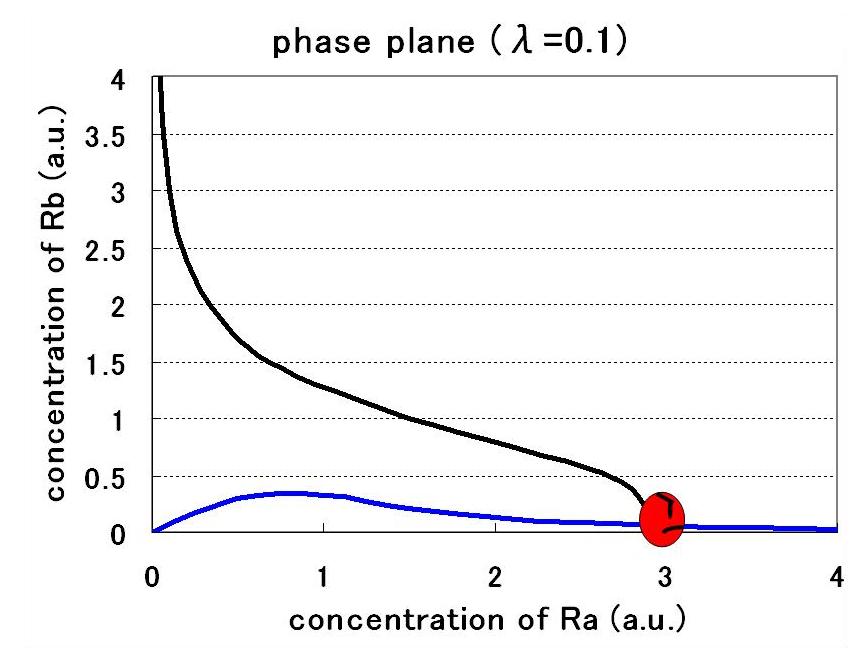
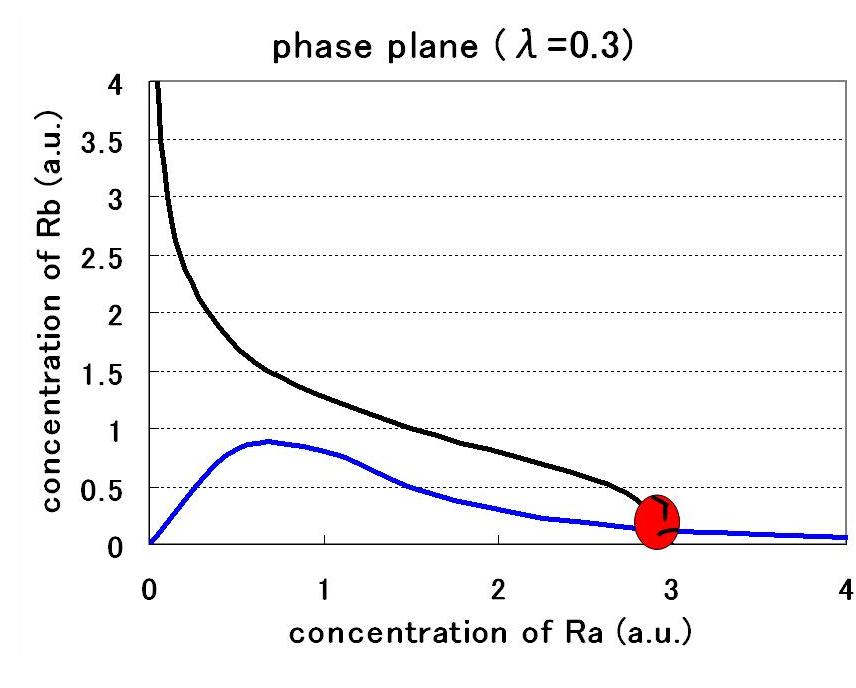
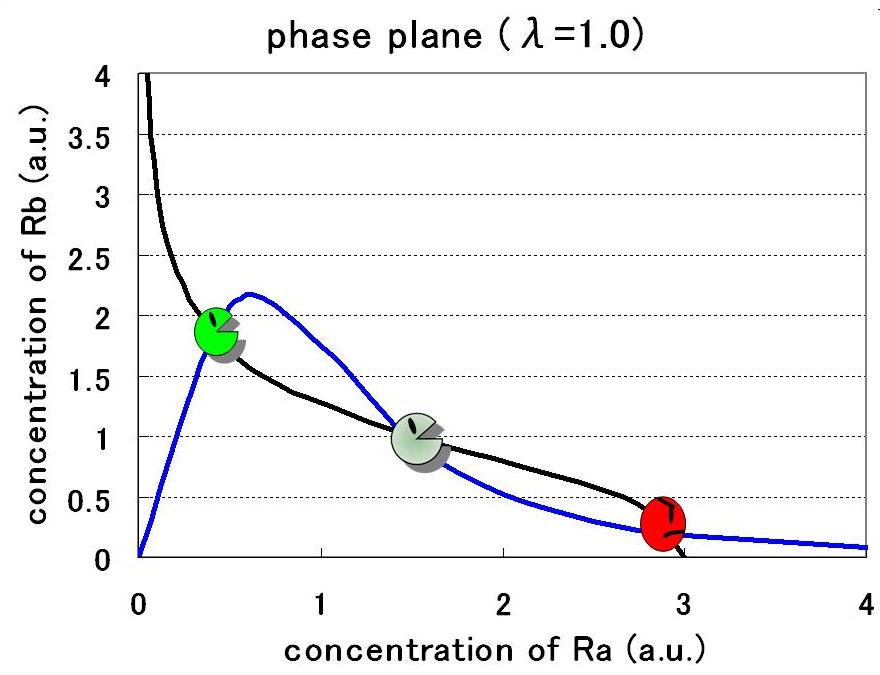
Step3.AHL-experssing model
<イントロ>
今度は,大腸菌の中からAHLを作り出す系に拡張する.
すると,nullclineが非対称になり,従来のトグルとは異なった相平面になる.
この際,新たなパラメータλが入ってくる.
パラメータセットによって,monoになったり,biになったりする.
Now develop this system to the one with cell-produced AHL.
This time, the nullcrine is assymetric and the phaseplane is unconventionally shaped.
Here the new parameter λ is introduced whether mono or bi of the system depends on the parameter sets
for more detail
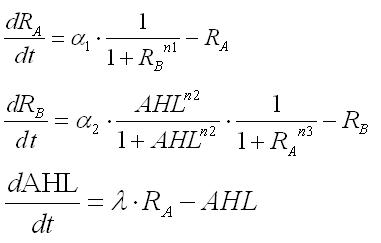
Step4.population model
<イントロ> 1個体から複数個体に拡張.AHLの式は,AHLの移動がfreelyと論文にあるので大腸菌内と外とを区別していない ここでも,相平面解析を行った.n個体の振る舞いであっても,その中の1個体に着目することで相平面解析を可能にした. この際,新たなパラメータとして個体数nがはいってくる.
Here the concentration of AHL is assumed the same inside and outside of a cell according to the description that AHL is freely permiable through cell membrane in the referenced articles. In the phaseplane analysis here is mede possible by focusing on an individual in the whole. In this case, the parameter n for the number of the cells is introduced.
ただし,deterministicなため全個体同じ動き.我々のモデルはこれではみれない. stochasticなシミュレーションが要求される.
However, all the individuals behave in the same way in this deterministic model. To see the bahavior different from each individual, it is necessary to use stocastic simulation.