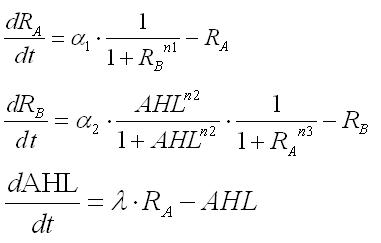Tokyo/Works/Formulation
From 2007.igem.org
| (25 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| - | |||
| - | <br>[[Tokyo/Formulation/1.toggle model |Step1]] | + | <br>[[Tokyo/Works|Works top]] 0.[[Tokyo/Works/Hybrid promoter|Hybrid promoter]] 1.[[Tokyo/Works/Formulation |Formulation]] 2.[[Tokyo/Works/Assay |Assay1]] 3.[[Tokyo/Works/Simulation |Simulation]] 4.[[Tokyo/Works/Assay2 |Assay2]] 5.[[Tokyo/Works/Future works |Future works]] |
| + | |||
| + | <br>[[Tokyo/Formulation/1.toggle model |Step1]] [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2]] [[Tokyo/Formulation/3.AHL-experssing model|Step3]] | ||
| + | <br> | ||
| + | |||
| + | |||
| + | == Numerical analysis for single cell == | ||
| + | |||
| + | |||
| + | == [[Tokyo/Formulation/1.toggle model |Step1. Single cell model:mutual inhibition ]] == | ||
| + | |||
| + | First, the qualitative nature was analyzed by simple dimensionless differential equations for this mutual inhibition system. The results of phase plane analysis for the equations suggested that the values of Hill coefficients were especially important in order that the system had the bistability corresponding to A and B states. | ||
| + | '''[[Tokyo/Formulation/1.toggle model | ==> see more]]''' | ||
<br> | <br> | ||
| - | |||
| - | |||
| - | |||
<br> [[Image:expression1-2.jpg|200px]] | <br> [[Image:expression1-2.jpg|200px]] | ||
| - | + | <!-- | |
| - | + | First, we saw the qualitative nature implied by simple dimentionless equations and found that the number of the stable points is one or two. Since our model must have A and B states, the number of its stable points should be two. | |
| - | <br> | + | <br>For the parameters required for this bistability, we have found that the expression rates and Hill coefficients are critical. |
| + | --> | ||
| + | == [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2. Single cell model with hybrid promoter]] == | ||
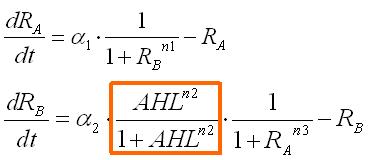
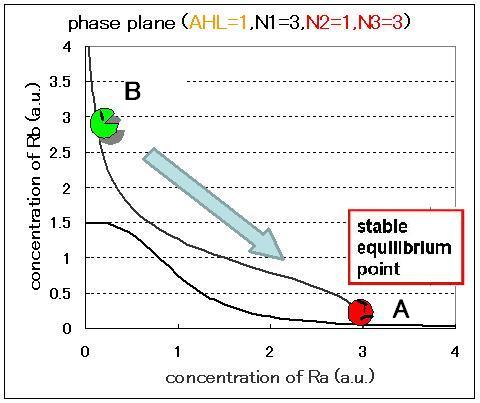
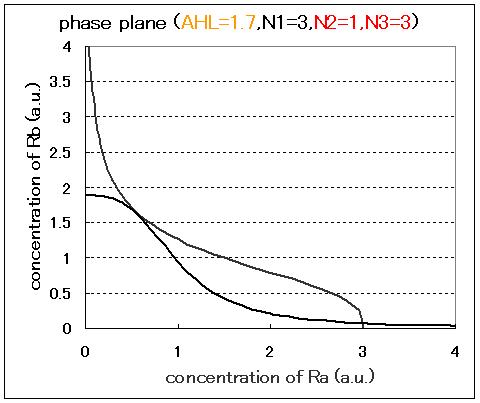
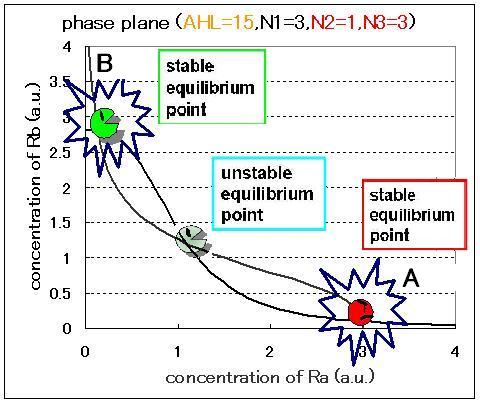
| + | Second, the effect of hybrid promoter was introduced into the single cell model. In the case of the model with hybrid promoter, the contribution from the repression of the promoter by LacI and that from the activation by AHL should be considered.; that is, the factor of AHL contribution was added to the differential equations for RB, resulting in the dependence of the phase plane on the AHL concentration. As a result of phase plane analysis for the equations, the system was monostable in the case of lower AHL concentration; whereas it was bistable in the case of higher AHL concentration. The values of Hill coefficients were important for the system bistability even in this case. | ||
| + | '''[[Tokyo/Formulation/2.toggle model with hybrid promoter | ==> see more]]''' | ||
| + | <br> | ||
| - | <br>[[Image: | + | <br>[[Image:expression2-4.jpg|280px|]][[Image:AHLresponse2-2.jpg|300px|]] |
| - | == [[Tokyo/Formulation/3.AHL-experssing model|Step3. | + | <br>[[Image:step2-4.JPG|300px|]][[Image:step2-5.JPG|300px|]][[Image:step2-6.JPG|300px|]] |
| + | |||
| + | |||
| + | <!-- | ||
| + | Factors of the hybrid promoter should be incorporated into the equations; that is, the term of the repression of toggle by LacI and that of the activation by AHL should be added. By these additions, the phase changes dependent on the amount of AHL. Lower concentration of AHL, monostable; while, higher one gives bistable. | ||
| + | --> | ||
| + | |||
| + | |||
| + | == [[Tokyo/Formulation/3.AHL-experssing model|Step3.Single cell model with hybrid promoter and cell-produced AHL]] == | ||
| + | |||
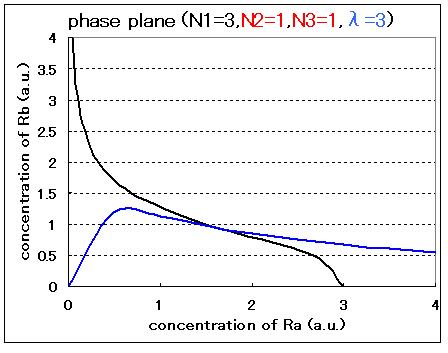
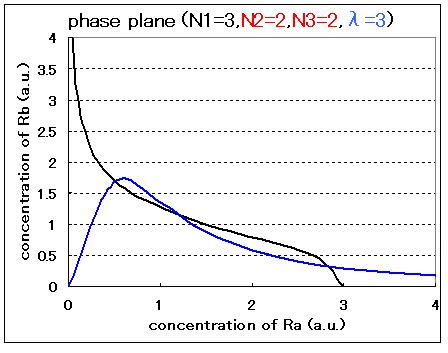
| + | Third, the system with hybrid promoter was expanded into the system using cell-produced AHL. Here, the new parameter λ was introduced to represent the producing rate of AHL by the promoter A. As a result of phase plane analysis, the values of Hill coefficients were important for the system bistability even in this case. '''[[Tokyo/Formulation/3.AHL-experssing model| ==> see more]]''' | ||
| + | <br>The results of the numerical analysis from Step1 to Step3 suggest the importance of the values of the Hill coefficients in this system. However, adjustments of Hill coefficients by DNA sequence modification are much more difficult than those of the other parameters (α1, α2, and λ); modifications in RBS -35 box, or -10 box allow change of those three parameters. We thus practically determined the values in the next wet experiments to confirm feasibility of our model. | ||
| + | |||
| + | <br>[[Image:expression3-1.jpg|300px|]] | ||
| + | <br>[[Image:Step3-3.JPG|300px|]][[Image:Step3-4.JPG|300px|]] | ||
| + | |||
| + | <!-- | ||
| + | <br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]] | ||
| + | --> | ||
| + | |||
| + | <!-- | ||
Now develop this system to the one with cell-produced AHL. | Now develop this system to the one with cell-produced AHL. | ||
This time, the nullcrine is assymetric and the phaseplane is unconventionally shaped. | This time, the nullcrine is assymetric and the phaseplane is unconventionally shaped. | ||
Here the new parameter λ is introduced whether monostalbe or bistable of the system depends on the velues of several parameters. | Here the new parameter λ is introduced whether monostalbe or bistable of the system depends on the velues of several parameters. | ||
| - | + | --> | |
| - | + | ||
| - | < | + | |
| + | |||
| + | <!-- | ||
| + | |||
== [[Tokyo/Formulation/4.population model|Step4. population model]] == | == [[Tokyo/Formulation/4.population model|Step4. population model]] == | ||
| Line 30: | Line 66: | ||
However, all the individuals behaved in the same way in this deterministic model. To see the bahavior of each individual cell, it is necessary to carry out stocastic simulation. | However, all the individuals behaved in the same way in this deterministic model. To see the bahavior of each individual cell, it is necessary to carry out stocastic simulation. | ||
| - | '''[[Tokyo/Formulation/4.population model| | + | '''[[Tokyo/Formulation/4.population model| ==> see more]]''' |
<br>[[Image:expression4-1.jpg|400px]] | <br>[[Image:expression4-1.jpg|400px]] | ||
| Line 41: | Line 77: | ||
<br>[[Image:expression5-1.jpg|400px]] | <br>[[Image:expression5-1.jpg|400px]] | ||
| - | |||
| - | |||
| - | With parameters from our [[Tokyo/Works/Assay |wet experiments]], we confirmed that our circuit with the new part can show “stable coexistence”'''see more リンク to simulation PAGE'''. | + | |
| + | <!-- | ||
| + | '''A preview of the latter part of this Wiki:'''--> | ||
| + | |||
| + | <!--With parameters from our [[Tokyo/Works/Assay |wet experiments]], we confirmed that our circuit with the new part can show “stable coexistence”'''see more リンク to simulation PAGE'''.--> | ||
| + | <!-- | ||
[[Image:3d-2.7-0.2.JPG|200px|left|thumb|Figure 5.2.A t=0.2(min)]] | [[Image:3d-2.7-0.2.JPG|200px|left|thumb|Figure 5.2.A t=0.2(min)]] | ||
[[Image:3d-2.7-30.JPG|200px|none|thumb|Figure 5.2.C t=30(min) '''success!! coexistence''']] | [[Image:3d-2.7-30.JPG|200px|none|thumb|Figure 5.2.C t=30(min) '''success!! coexistence''']] | ||
| + | .--> | ||
| + | <!-- | ||
===[[Tokyo/Formulation/5.stochastic differential equation model with poisson random variables/ A and B coexistence movie/ |Click!! movie here!!]]=== | ===[[Tokyo/Formulation/5.stochastic differential equation model with poisson random variables/ A and B coexistence movie/ |Click!! movie here!!]]=== | ||
| + | .--> | ||
== == | == == | ||
<br> [[Tokyo/Works/Hybrid promoter|Before(Hybrid promoter)]] << [[Tokyo/Works/Formulation |Formulation]] >> [[Tokyo/Formulation/1.toggle model|Formulation Step.1]] >>>> [[Tokyo/Works/Assay|Next(Assay1)]] | <br> [[Tokyo/Works/Hybrid promoter|Before(Hybrid promoter)]] << [[Tokyo/Works/Formulation |Formulation]] >> [[Tokyo/Formulation/1.toggle model|Formulation Step.1]] >>>> [[Tokyo/Works/Assay|Next(Assay1)]] | ||
Latest revision as of 05:09, 27 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
Numerical analysis for single cell
Step1. Single cell model:mutual inhibition
First, the qualitative nature was analyzed by simple dimensionless differential equations for this mutual inhibition system. The results of phase plane analysis for the equations suggested that the values of Hill coefficients were especially important in order that the system had the bistability corresponding to A and B states.
==> see more
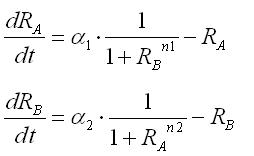
Step2. Single cell model with hybrid promoter
Second, the effect of hybrid promoter was introduced into the single cell model. In the case of the model with hybrid promoter, the contribution from the repression of the promoter by LacI and that from the activation by AHL should be considered.; that is, the factor of AHL contribution was added to the differential equations for RB, resulting in the dependence of the phase plane on the AHL concentration. As a result of phase plane analysis for the equations, the system was monostable in the case of lower AHL concentration; whereas it was bistable in the case of higher AHL concentration. The values of Hill coefficients were important for the system bistability even in this case.
==> see more
Step3.Single cell model with hybrid promoter and cell-produced AHL
Third, the system with hybrid promoter was expanded into the system using cell-produced AHL. Here, the new parameter λ was introduced to represent the producing rate of AHL by the promoter A. As a result of phase plane analysis, the values of Hill coefficients were important for the system bistability even in this case. ==> see more
The results of the numerical analysis from Step1 to Step3 suggest the importance of the values of the Hill coefficients in this system. However, adjustments of Hill coefficients by DNA sequence modification are much more difficult than those of the other parameters (α1, α2, and λ); modifications in RBS -35 box, or -10 box allow change of those three parameters. We thus practically determined the values in the next wet experiments to confirm feasibility of our model.
Before(Hybrid promoter) << Formulation >> Formulation Step.1 >>>> Next(Assay1)