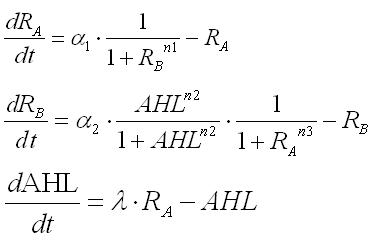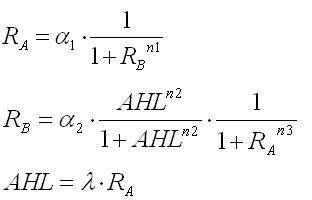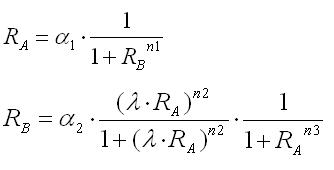Tokyo/Formulation/3.AHL-experssing model
From 2007.igem.org
(→Step.3 Single cell model with hybrid promoter and cell-produced AHL) |
|||
| (3 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| - | <br>[[Tokyo/Works|Works top]] | + | <br>[[Tokyo/Works|Works top]] 0.[[Tokyo/Works/Hybrid promoter|Hybrid promoter]] '''1.[[Tokyo/Works/Formulation |Formulation]]''' 2.[[Tokyo/Works/Assay |Assay1]] 3.[[Tokyo/Works/Simulation |Simulation]] 4.[[Tokyo/Works/Assay2 |Assay2]] 5.[[Tokyo/Works/Future works |Future works]] |
| - | <br><br>[[Tokyo/Formulation/1.toggle model |Step1]] | + | <br><br>[[Tokyo/Formulation/1.toggle model |Step1]] [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2]] [[Tokyo/Formulation/3.AHL-experssing model|Step3]] |
<br> | <br> | ||
== Step.3 Single cell model with hybrid promoter and cell-produced AHL == | == Step.3 Single cell model with hybrid promoter and cell-produced AHL == | ||
| - | <br>The differential | + | <br>The differential equations of the system considering AHL produced by E.coli themselves were given as |
<br> [[Image:expression3-4.jpg|400px|left|thumb|Ex 3-1]][[Image:parameter3-1.jpg|200px|none|thumb|Table 3]] | <br> [[Image:expression3-4.jpg|400px|left|thumb|Ex 3-1]][[Image:parameter3-1.jpg|200px|none|thumb|Table 3]] | ||
| Line 29: | Line 29: | ||
<br>[[Image:step3-6.JPG|300px|thumb|none|Figure 3.1.D]] | <br>[[Image:step3-6.JPG|300px|thumb|none|Figure 3.1.D]] | ||
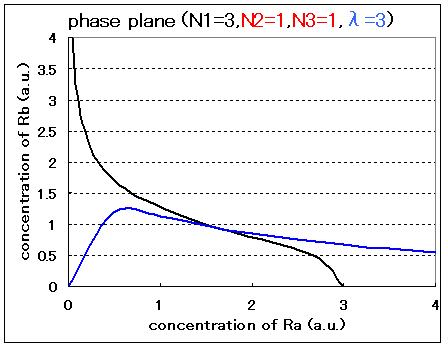
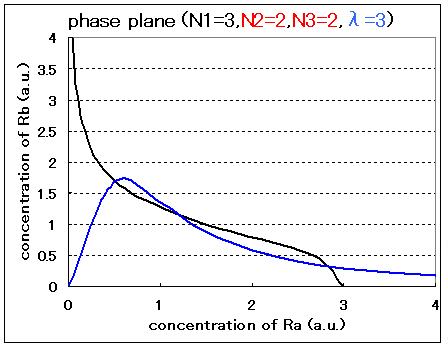
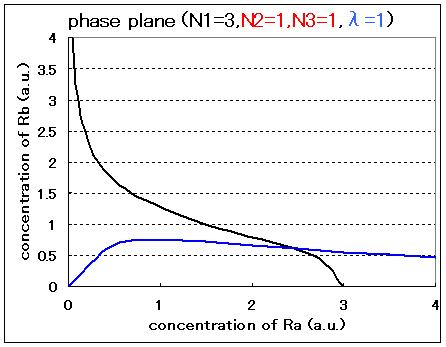
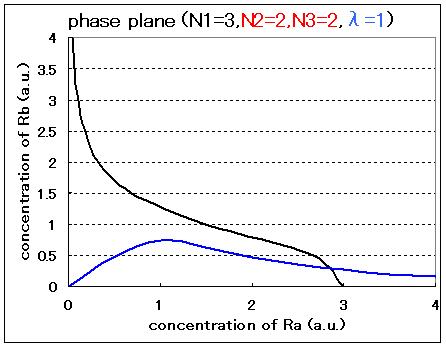
| - | Fig3.1.A and B indicated that in case of N2=1,N3=1,the phase plane was monostable | + | Comparison between Fig3.1.A and B indicated that Hill coefficients are critical parameters even in the cell-produced AHL model. In the case of N2=1, N3=1, and λ=3, the phase plane was monostable. In contrast, in the case of N2=2, N3=2, and λ=3, the phase plane was bistable. |
| + | <br> In the cases of λ=1 (Fig.3.1.C and D), the system can not take bistability even if the values of Hill coefficients are changed. For the implementation of the circuit in a cell, the parameter λ should be controlled by changing the RBSs and/or promoter sequences of LuxR. | ||
| + | |||
<!-- | <!-- | ||
Latest revision as of 05:00, 27 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
Step1 Step2 Step3
Step.3 Single cell model with hybrid promoter and cell-produced AHL
The differential equations of the system considering AHL produced by E.coli themselves were given as
These equations were normalized as follows:
In the steady state,time derivatives are zero.As a result,the nullclines of this system were derived as
By substituting the third equation into the second,the nullclines for Ra and Rb were obtained as
Therefore, the phase plane of this system can be plotted as Fig.3.1.A-D and the number of equilibrium points were decided by the value of the parameters:
Comparison between Fig3.1.A and B indicated that Hill coefficients are critical parameters even in the cell-produced AHL model. In the case of N2=1, N3=1, and λ=3, the phase plane was monostable. In contrast, in the case of N2=2, N3=2, and λ=3, the phase plane was bistable.
In the cases of λ=1 (Fig.3.1.C and D), the system can not take bistability even if the values of Hill coefficients are changed. For the implementation of the circuit in a cell, the parameter λ should be controlled by changing the RBSs and/or promoter sequences of LuxR.
Step.3 >> Formulation top