Tokyo/Works/Formulation
From 2007.igem.org
| Line 4: | Line 4: | ||
<br>[[Tokyo/Formulation/1.toggle model |Step1]] [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2]] [[Tokyo/Formulation/3.AHL-experssing model|Step3]] [[Tokyo/Formulation/4.population model|Step4]] [[Tokyo/Formulation/5.stochastic differential equation model with poisson random variables|Step5]] | <br>[[Tokyo/Formulation/1.toggle model |Step1]] [[Tokyo/Formulation/2.toggle model with hybrid promoter |Step2]] [[Tokyo/Formulation/3.AHL-experssing model|Step3]] [[Tokyo/Formulation/4.population model|Step4]] [[Tokyo/Formulation/5.stochastic differential equation model with poisson random variables|Step5]] | ||
<br> | <br> | ||
| - | == [[Tokyo/Formulation/1.toggle model |Step1. | + | == [[Tokyo/Formulation/1.toggle model |Step1. Single cell model:mutual inhibition ]] == |
| - | First, | + | |
| - | + | First, the qualitative nature was analyzed by simple dimensionless differential equations for this mutual inhibition system. The results of phase plane analysis for the equations suggested that the values of Hill coefficients were especially important in order that the system had the bistability corresponding to A and B states. | |
| + | '''[[Tokyo/Formulation/1.toggle model | ⇒ see more]]''' | ||
<br> [[Image:expression1-2.jpg|200px]] | <br> [[Image:expression1-2.jpg|200px]] | ||
| - | == [[Tokyo/Formulation/2. | + | <!-- |
| - | + | First, we saw the qualitative nature implied by simple dimentionless equations and found that the number of the stable points is one or two. Since our model must have A and B states, the number of its stable points should be two. | |
| + | <br>For the parameters required for this bistability, we have found that the expression rates and Hill coefficients are critical. | ||
| + | --> | ||
| + | |||
| + | |||
| + | == [[Tokyo/Formulation/2.Single cell model with hybrid promoter |Step2. Single cell model with hybrid promoter]] == | ||
| + | |||
| + | Second, the effect of hybrid promoter was introduced into the single cell model. In the case of the model with hybrid promoter, the contribution from the repression of the promoter by LacI and that from the activation by AHL should be considered.; that is, the factor of AHL contribution was added to the differential equations for RB, resulting in the dependence of the phase plane on the AHL concentration. As a result of phase plane analysis for the equations, the system was monostable in the case of lower AHL concentration; whereas it was bistable in the case of higher AHL concentration. The values of Hill coefficients were important for the system bistability even in this case. | ||
| + | '''[[Tokyo/Formulation/2.toggle model with hybrid promoter | ⇒ see more]]''' | ||
<br>[[Image:expression2-4.jpg|300px|]][[Image:AHLresponse2-2.jpg|300px|]] | <br>[[Image:expression2-4.jpg|300px|]][[Image:AHLresponse2-2.jpg|300px|]] | ||
| + | <br>[[Image:AHLresponse2-3.jpg|330px|]][[Image:AHLresponse2-4.jpg|300px|]][[Image:AHLresponse2-5.jpg|300px|]] | ||
| + | <!-- | ||
| + | Factors of the hybrid promoter should be incorporated into the equations; that is, the term of the repression of toggle by LacI and that of the activation by AHL should be added. By these additions, the phase changes dependent on the amount of AHL. Lower concentration of AHL, monostable; while, higher one gives bistable. | ||
| + | --> | ||
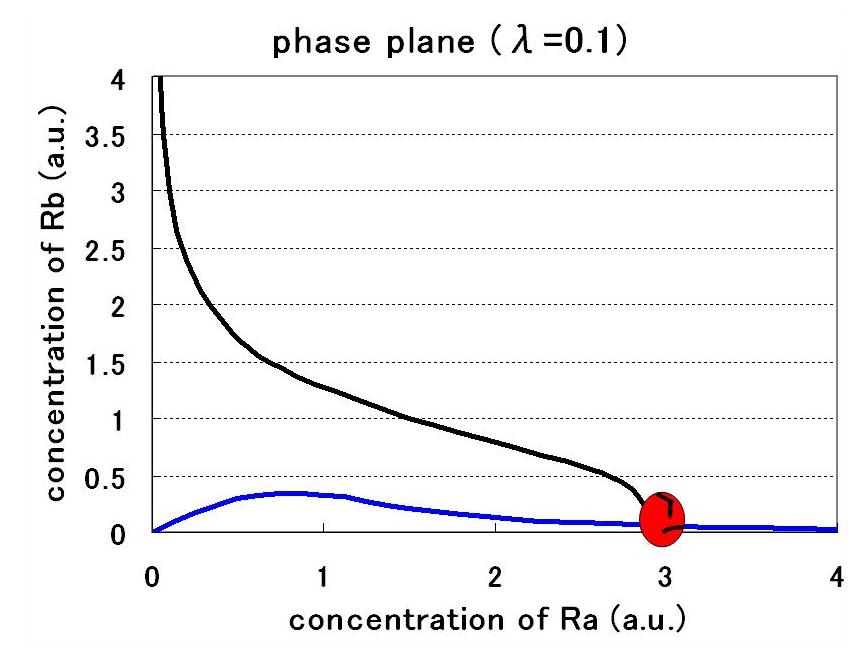
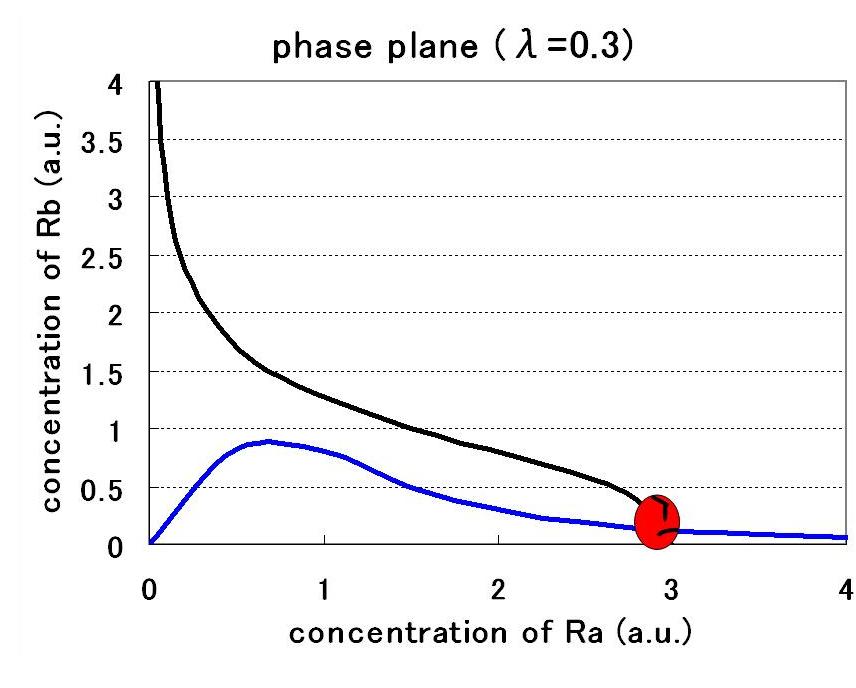
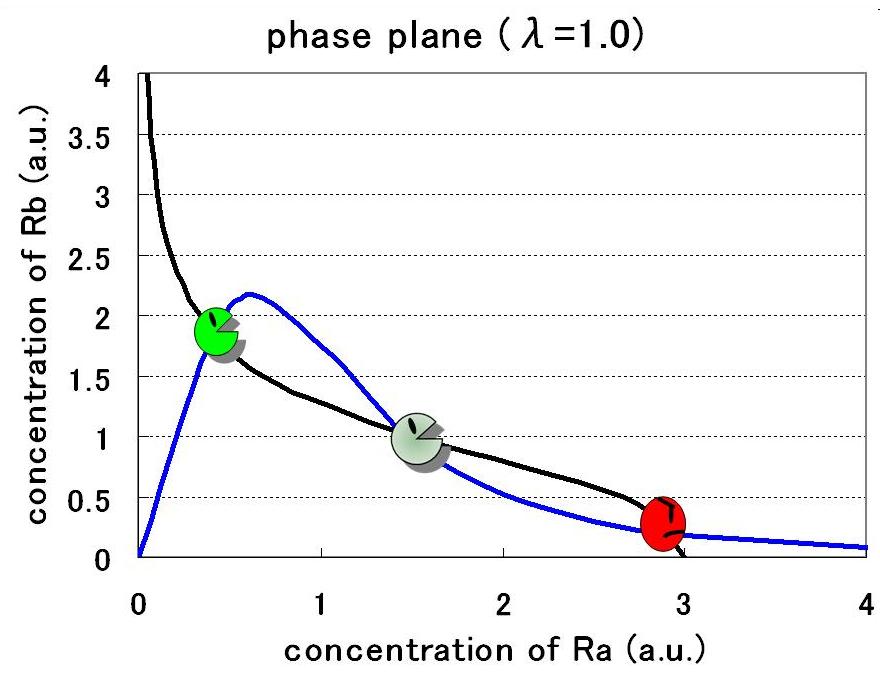
| - | + | == [[Tokyo/Formulation/3.Single cell model with hybrid promoter and cell-produced AHL|Step3.Single cell model with hybrid promoter and cell-produced AHL]] == | |
| - | + | Third, the system with hybrid promoter was expanded into the system using cell-produced AHL. Here, the new parameter λ was introduced to represent the producing rate of AHL by the promoter A. As a result of phase plane analysis, the values of Hill coefficients were important for the system bistability even in this case. The results of the numerical analysis from Step1 to Step3 suggests the importance of the values of the Hill coefficients in this system, so that we practically determined the values in the next wet experiments | |
| - | + | ||
| - | + | ||
| - | + | ||
'''[[Tokyo/Formulation/3.AHL-experssing model| ⇒ see more]]''' | '''[[Tokyo/Formulation/3.AHL-experssing model| ⇒ see more]]''' | ||
<br>[[Image:expression3-1.jpg|300px|]] | <br>[[Image:expression3-1.jpg|300px|]] | ||
<br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]] | <br>[[Image:Phaseplane3-1.jpg|300px|]] [[Image:Phaseplane3-2.jpg|300px|]] [[Image:Phaseplane3-3.jpg|300px|]] | ||
| + | |||
| + | |||
| + | <!-- | ||
| + | Now develop this system to the one with cell-produced AHL. | ||
| + | This time, the nullcrine is assymetric and the phaseplane is unconventionally shaped. | ||
| + | Here the new parameter λ is introduced whether monostalbe or bistable of the system depends on the velues of several parameters. | ||
| + | --> | ||
Revision as of 17:50, 26 October 2007
Works top 0.Hybrid promoter 1.Formulation 2.Assay1 3.Simulation 4.Assay2 5.Future works
Step1. Single cell model:mutual inhibition
First, the qualitative nature was analyzed by simple dimensionless differential equations for this mutual inhibition system. The results of phase plane analysis for the equations suggested that the values of Hill coefficients were especially important in order that the system had the bistability corresponding to A and B states.
⇒ see more
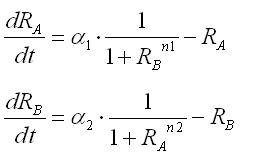
Step2. Single cell model with hybrid promoter
Second, the effect of hybrid promoter was introduced into the single cell model. In the case of the model with hybrid promoter, the contribution from the repression of the promoter by LacI and that from the activation by AHL should be considered.; that is, the factor of AHL contribution was added to the differential equations for RB, resulting in the dependence of the phase plane on the AHL concentration. As a result of phase plane analysis for the equations, the system was monostable in the case of lower AHL concentration; whereas it was bistable in the case of higher AHL concentration. The values of Hill coefficients were important for the system bistability even in this case.
⇒ see more
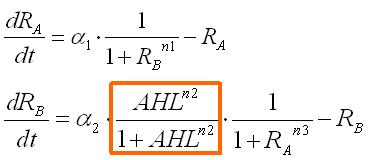


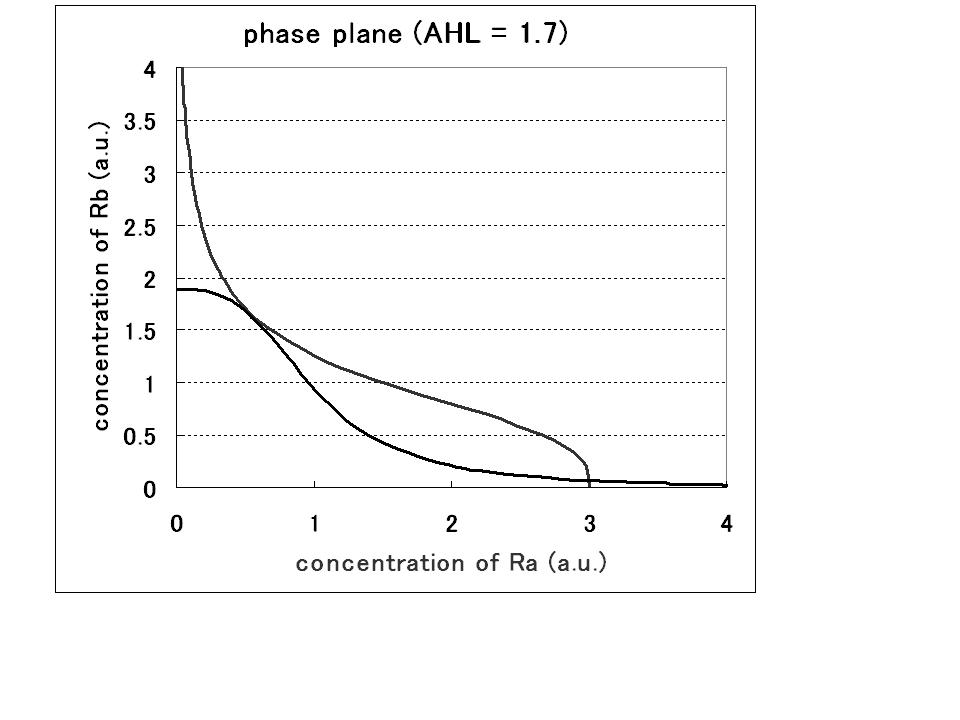
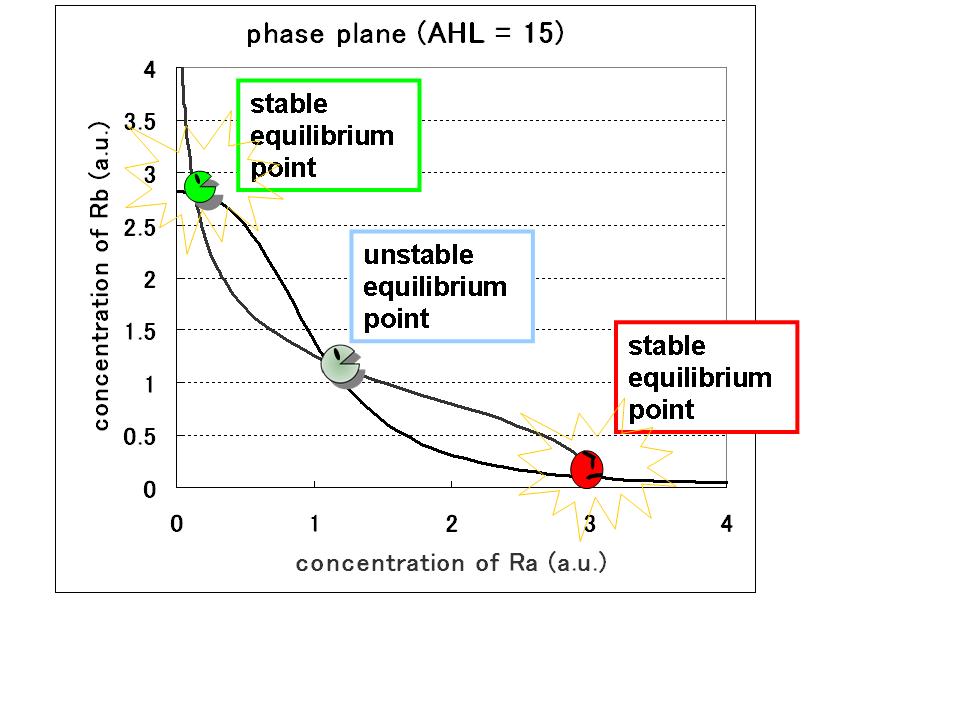
Step3.Single cell model with hybrid promoter and cell-produced AHL
Third, the system with hybrid promoter was expanded into the system using cell-produced AHL. Here, the new parameter λ was introduced to represent the producing rate of AHL by the promoter A. As a result of phase plane analysis, the values of Hill coefficients were important for the system bistability even in this case. The results of the numerical analysis from Step1 to Step3 suggests the importance of the values of the Hill coefficients in this system, so that we practically determined the values in the next wet experiments
⇒ see more
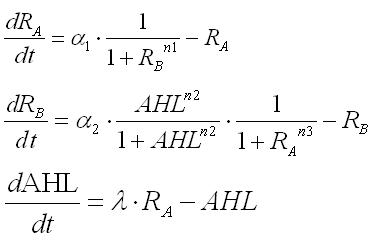
Before(Hybrid promoter) << Formulation >> Formulation Step.1 >>>> Next(Assay1)