Revision as of 23:03, 25 October 2007

Cell-Free: Characterisation

Purpose

In this section we analyse the data we have obtained on the cell-free chassis using GFP as the reporter. We show that the classic model for the synthesis of a protein by a constitutive promoter is not adapted and introduce a new model where synthesis is curbed by the resources left in the system. Finally we estimate the parameters of this new model from our data and show that it yields a much better fit.

Prior Knowledge

pTet and pT7 are constitutive promoters that are commonly used in vivo for E. coli
Tests in vitro have demonstrated that they also work on the cell-free chassis
Manufacturer specifications: the solution has been optimised so the degradation of proteins is minimal. We therefore expect our analysis to find very small degradation terms

Available Data

We need as many data as possible and also data that are as varied as possible (data with similar behaviour will lead to the selection of a model that is too simple to predict all the behaviours that can be generated by the chassis).

For this section we will use

the data collected with pTet at 4,15,25 and 37 degrees (link to wiki page) that exhibit a linear behaviour
the pT7 data at 4 and 25 degrees (link to wiki page) that exhibit a saturated behaviour.

We use the calibration curve of GFP (link to wiki page) to convert the fluorescence data into concentrations (in this case the concentrations were express in nanomols/l).

Axes: time in hours
FP is the concentration of Fluorescent Protein (GFP here) in nanomol/l

The Classic Model

To analyse our data we use the classic approach that consists of modelling the evolution with time of the concentrations of the product of interest. In this case the model is the simplest we can imagine:

We have only one protein GFP
It is constitutively synthesized at a constant synthesis rate K. K depends on the promoter that is used and ourdata show that it is also temperature-dependent
The protein is then degraded. This degradation term δ depends on the protein and on the chassis. We can assume the impact of temperature to be negligible.

The differential equation governing the evolution of X , the concentration of GFP is

In all cases the initial concentration of GFP was X₀ = 0. The solution of the equation is known explicitly. It is

@@ Line 3: / Line 3: @@
 = Cell-Free: Characterisation =
-The characterisation of parts and devices in the [http://partsregistry.org/Main_Page Registry of Standard Biological Parts] have have been considered in terms of rate of gene expression in the units Polymerase per Second (PoPS) or Ribosome per Second (RiPS). However the characterisation of the cell-free chassis housing the expression machinery has not been considered up till now. Our team has defined some parameters as well as partially characterised the various systems that will help us better understand the characteristics and limitations associated with CFS in general.
-For a definition of chassis specifications, click [http://partsregistry.org/Chassis/Cell-Free_Systems here].
+== Purpose ==
+In this section we analyse the data we have obtained on the cell-free chassis using GFP as the reporter. We show that the classic model for the synthesis of a protein by a constitutive promoter is not adapted and introduce a new model where synthesis is curbed by the resources left in the system. Finally we estimate the parameters of this new model from our data and show that it yields a much better fit.
-Follow the links below for more information on their characterisation:
+== Prior Knowledge ==
+* pTet and pT7 are constitutive promoters that are commonly used ''in vivo'' for ''E. coli''
+* [[Imperial/Wet_Lab/Protocols/asdasdasf|Tests]] ''in vitro''  have demonstrated that they also work on the cell-free chassis
+* Manufacturer specifications: the solution has been optimised so the degradation of proteins is minimal. We therefore expect our analysis to find very small degradation terms
-* [http://partsregistry.org/Chassis/Cell-Free_Systems/Homemade_E.coli_S30 Homemade ''E. coli'' S30]
+== Available Data ==
-* [http://partsregistry.org/Chassis/Cell-Free_Systems/Commercial_E.coli_S30 Commercial ''E. coli'' S30]
+We need as many data as possible and also data that are as varied as possible (data with similar behaviour will lead to the selection of a model  that is too simple to predict all the behaviours that can be generated by the chassis).
-* [http://partsregistry.org/Chassis/Cell-Free_Systems/Commercial_E.coli_T7_S30 Commercial ''E. coli'' T7 S30]
-* [http://partsregistry.org/Chassis/Cell-Free_Systems/Vesicle Vesicle Encapsulation]
-<br clear="all">
+For this section we will use
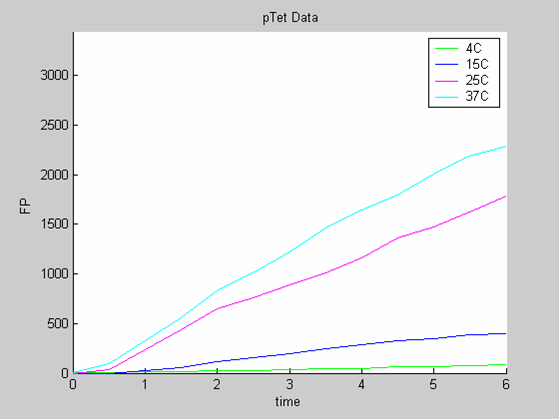
+* the data collected with pTet at 4,15,25 and 37 degrees (link to wiki page) that exhibit a linear behaviour
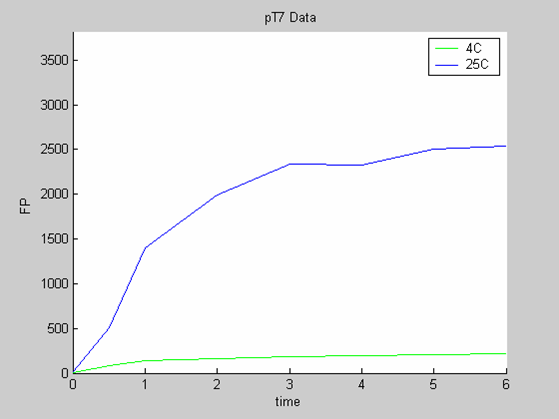
+* the pT7 data at 4 and 25 degrees   (link to wiki page) that exhibit a saturated behaviour.
-<center> [https://2007.igem.org/Imperial/Cell-Free/Contribution << Our Contribution ] | Characterisation | [https://2007.igem.org/Imperial/Cell-Free/Applications Applications >>]</center>
+We use the calibration curve of GFP (link to wiki page)   to convert the fluorescence data into concentrations (in this case the concentrations were express in nanomols/l).
+{| align="center"
+|-
+||[[Image:IC07_CFSpTet.png|left|400px]]
+||[[Image:IC07_CFSpT7.png|left|400px]]
+|}
+''Axes: time in hours''<br>
+''FP is the concentration of Fluorescent Protein (GFP here) in nanomol/l''
+== The Classic Model ==
+To analyse our data we use the classic approach that consists of modelling the evolution with time of the concentrations of the product of interest.
+In this case the model is the simplest we can imagine:
+* We have only one protein GFP
+* It is constitutively synthesized at a constant synthesis rate K. K depends on the promoter that is used and ourdata show that it is also temperature-dependent
+* The protein is then degraded. This degradation term δ depends on the protein and on the chassis. We can assume the impact of temperature to be negligible.
+The differential equation governing the evolution of X , the concentration of GFP is
+[[Image:IC07_CFSeqn1.png|center|100px]]
+In all cases the initial concentration of GFP was X<sub>0</sub> = 0. The solution of the equation is known explicitly. It is
+[[Image:IC07_CFSeqn2.png|center|140px]]

Views

Personal tools