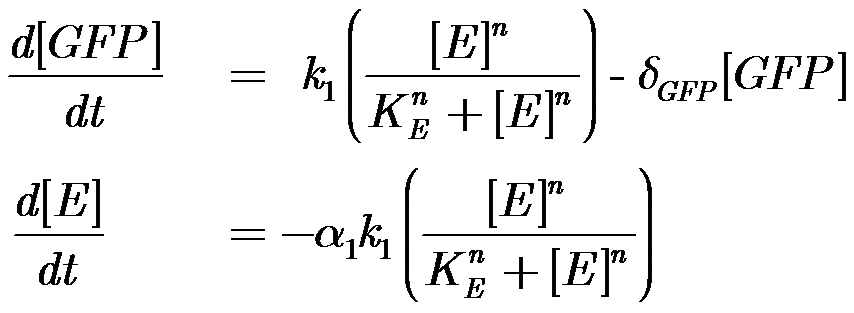Imperial/Cell by Date/Modelling
From 2007.igem.org
(→Modelling the spoilage of Aerobically Stored Ground Hamburger Meat) |
(→Modelling the spoilage of Aerobically Stored Ground Hamburger Meat) |
||
| Line 27: | Line 27: | ||
Previous work has been carried out to model the spoilage of ground beef by living organisms. | Previous work has been carried out to model the spoilage of ground beef by living organisms. | ||
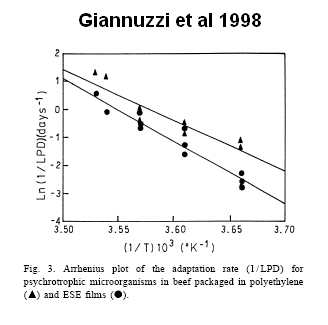
| - | Above in figure 1 | + | Above, in figure 1, is a model developed by Koutsoumanis <sup>[[#References|1]]</sup> who colesly fit the behaviour of the spoilage organism we are interested in, Pseudomonas, under dynamic temperature conditions. One of the key conclusions drawn from this model is the almost instantaneous response time of the Pseudomonas' growth parameter. The result of this is that our system needs to have a quick respone time to correctly report the temperature history of the beef. |
| - | Koutsoumanis' model, and also one Giannuzzi developed <sup>[[#References|2]]</sup> are both based on the Gompertz model. This model allows some insight into the mechanisms of ground beef spoilage. In particular through manipulation of the Gompertz Parameters and assuming | + | Koutsoumanis' model, and also one Giannuzzi developed <sup>[[#References|2]]</sup> are both based on the Gompertz model. This model allows some insight into the mechanisms of ground beef spoilage. In particular through manipulation of the Gompertz Parameters and assuming an Arrhenius-type relationship between the Pseudomonas' growth parameter and temperature, we can infer the Activation Energy(E<sub>a</sub> of the spoilage reaction. <sup>[[#References|3]]</sup> This is shown in figure 2, in which a strongly linear behaviour allows us to continue with our Arrhenius assumption and extract the Activation Energy of the spoilage reaction. As given in our specifications, the Activation Energy for ground meat seems to be around 30kJ/mol. The result of this as per Leak's work is that our system needs to have a similar activation energy. We hope to determine our system activation energy in the same manner Giannuzzi determined that of Pseudomonas'. |
==Modelling our system: Energy-limited constitutive expression by pTET-mut3BGFP== | ==Modelling our system: Energy-limited constitutive expression by pTET-mut3BGFP== | ||
Revision as of 03:25, 26 October 2007

Cell by Date: Modelling
Modelling the spoilage of Aerobically Stored Ground Hamburger Meat
Previous work has been carried out to model the spoilage of ground beef by living organisms. Above, in figure 1, is a model developed by Koutsoumanis 1 who colesly fit the behaviour of the spoilage organism we are interested in, Pseudomonas, under dynamic temperature conditions. One of the key conclusions drawn from this model is the almost instantaneous response time of the Pseudomonas' growth parameter. The result of this is that our system needs to have a quick respone time to correctly report the temperature history of the beef.
Koutsoumanis' model, and also one Giannuzzi developed 2 are both based on the Gompertz model. This model allows some insight into the mechanisms of ground beef spoilage. In particular through manipulation of the Gompertz Parameters and assuming an Arrhenius-type relationship between the Pseudomonas' growth parameter and temperature, we can infer the Activation Energy(Ea of the spoilage reaction. 3 This is shown in figure 2, in which a strongly linear behaviour allows us to continue with our Arrhenius assumption and extract the Activation Energy of the spoilage reaction. As given in our specifications, the Activation Energy for ground meat seems to be around 30kJ/mol. The result of this as per Leak's work is that our system needs to have a similar activation energy. We hope to determine our system activation energy in the same manner Giannuzzi determined that of Pseudomonas'.
Modelling our system: Energy-limited constitutive expression by pTET-mut3BGFP
| Parameter | Description |
|---|---|
| k1 | Maximal constitutive transcription by pTET |
| KE | Half-Saturation Coefficient for Energy Hill function |
| n | Positive Cooperativity Coefficient (Hill-coefficient) |
| delta;GFP | Decay constant of mut3BGFP |
here δGFP = 0.0005
With some understanding of how Pseudomonas spoils aerobically stored ground beef, it is really important for us to gain some understanding of how our sytem behaves in similar scenarios, to the models developed by Koutsoumanis and Giannuzi, in order to extract the same parameters.
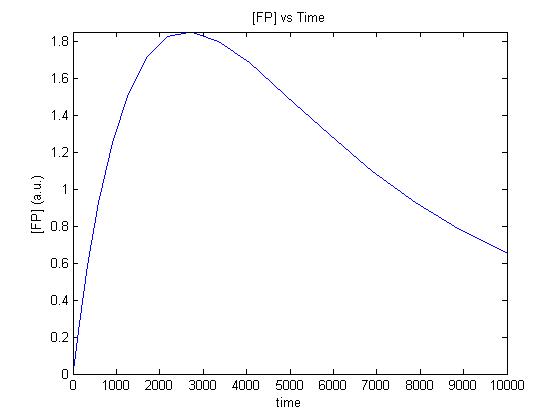
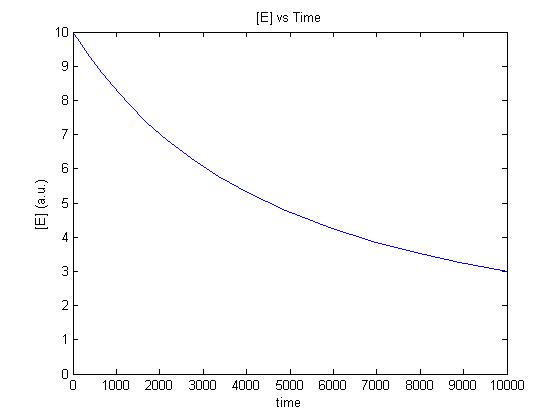
For isothermal conditions we have been able to develop some simple models of the gene expression of our sytem, with a strong dependance on energy depletion, as we believe this is the major limiting factor of our system.
As seen above in figures 3 and 4, with energy depletion as our major limiting factor we expect the concentration of our reporter gene to increase to a peak and then, as energy runs out, expressoin is curbed and decay of our reporter dominates, giving an exponential-like decay.
The m-files used in the following simulations can be accessed on our Software page.
References
- [http://iufost.edpsciences.org/index.php?option=article&access=standard&Itemid=129&url=/articles/iufost/pdf/2006/01/iufost06000765.pdf Koutsoumanis K, Stamatiou A, Skandamis P, Nychas GJ. Development of a Microbial Model for the Combined Effect of Temperature and pH on Spoilage of Ground Meat, and Validation of the Model under Dynamic Temperature Conditions. Appl Environ Microbiol. 2006 Jan;72(1):124-34.]
- [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6T7K-3S3M25D-B&_user=217827&_coverDate=01%2F06%2F1998&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct=C000011279&_version=1&_urlVersion=0&_userid=217827&md5=80630ba21fbc6869b9f5179d334734da Giannuzzi L, Pinotti A, Zaritzky N. Mathematical modelling of microbial growth in packaged refrigerated beef stored at different temperatures. Int J Food Microbiol. 1998 Jan 6;39(1-2):101-10.]
- [http://66.102.1.104/scholar?hl=en&lr=&q=cache:thi6BTIW1YMJ:www.vitsab.com/PDF/V507.pdf+TTI+Beef+Activation+Energy Leak, F.W. (2000): Quality changes in Ground beef during distribution and storage, and determination of Time- Temperature-Indicator (TTI) charakteristic of ground beef University of Florida Institute of food and Agricultural Sciences Internet: www.vitsab.com, Stand: April 2003]
- [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6T7K-4CP14B0-2&_user=217827&_coverDate=11%2F15%2F2004&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct=C000011279&_version=1&_urlVersion=0&_userid=217827&md5=cf92d0ca2566b940589f521601b36eca Lopez, 2004 : Critique of Gompertz Model]
- [http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6T7K-485PCG5-3&_user=217827&_coverDate=11%2F01%2F2003&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct=C000011279&_version=1&_urlVersion=0&_userid=217827&md5=608c478638b6d194576d0f151be2223f Huang, 2003 Simulation of a Similar Problem using Gompertz Model]